神经网络和深度学习[1-2]
神经网络和深度学习[1-3]
神经网络和深度学习[1-4]
改善深层神经网络:超参数调试、正则化以及优化【2-1】
改善深层神经网络:超参数调试、正则化以及优化【2-2】
改善深层神经网络:超参数调试、正则化以及优化【2-3】
结构化机器学习项目 3
Ng的深度学习视频笔记,长期更新
1.2 边缘检测示例
在深度神经网络中的前几层检测一些边缘特征,后面的层可能检测到物体的部分,更靠后的层可能检测到完整的物体,如下面这个人脸的例子:
给出下面这样一张图: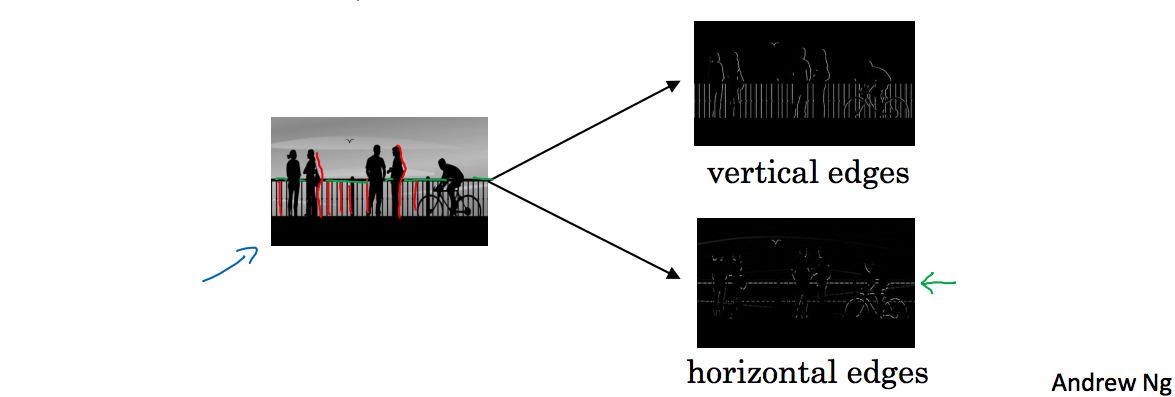
如果让电脑来做,首先可能是检测图片中的垂直边缘,比如这样图片中的栏杆,行人等都是垂直边缘检测器的输出。下面一张图是检测水平边缘,比如栏杆的横线。那么如何检测到这些线呢?
先讲一下过滤器,如下图所示: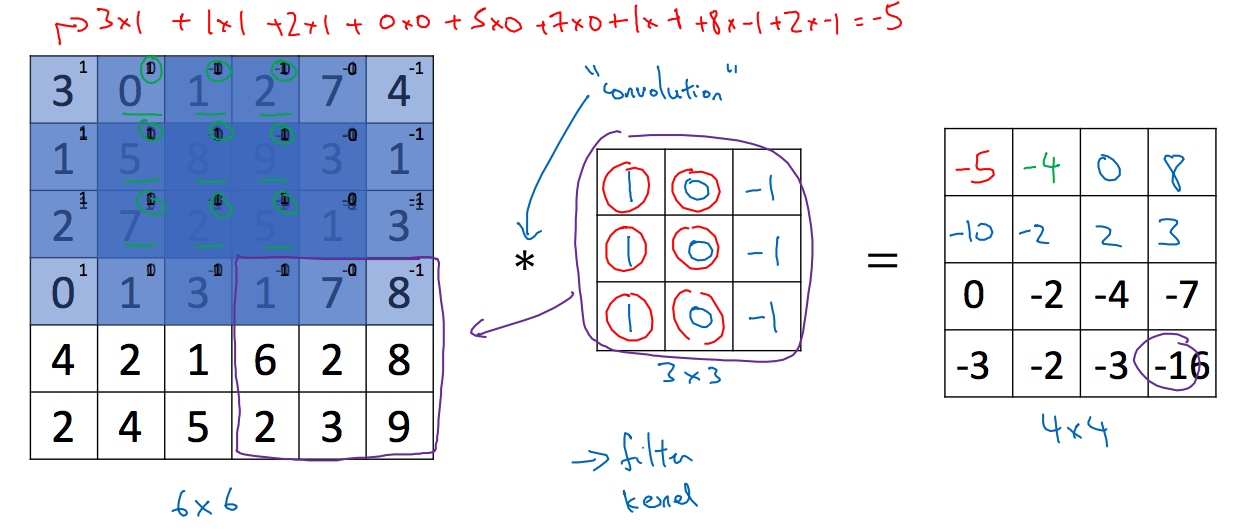
这里左边是一个6x6的图片矩阵,中间的是3x3的过滤器,卷积的结果是一个4x4的矩阵,计算过程就是将图像矩阵和过滤器求和,那么这个为什么就能检测到垂线呢,我们继续看下面这个例子,如下图所示: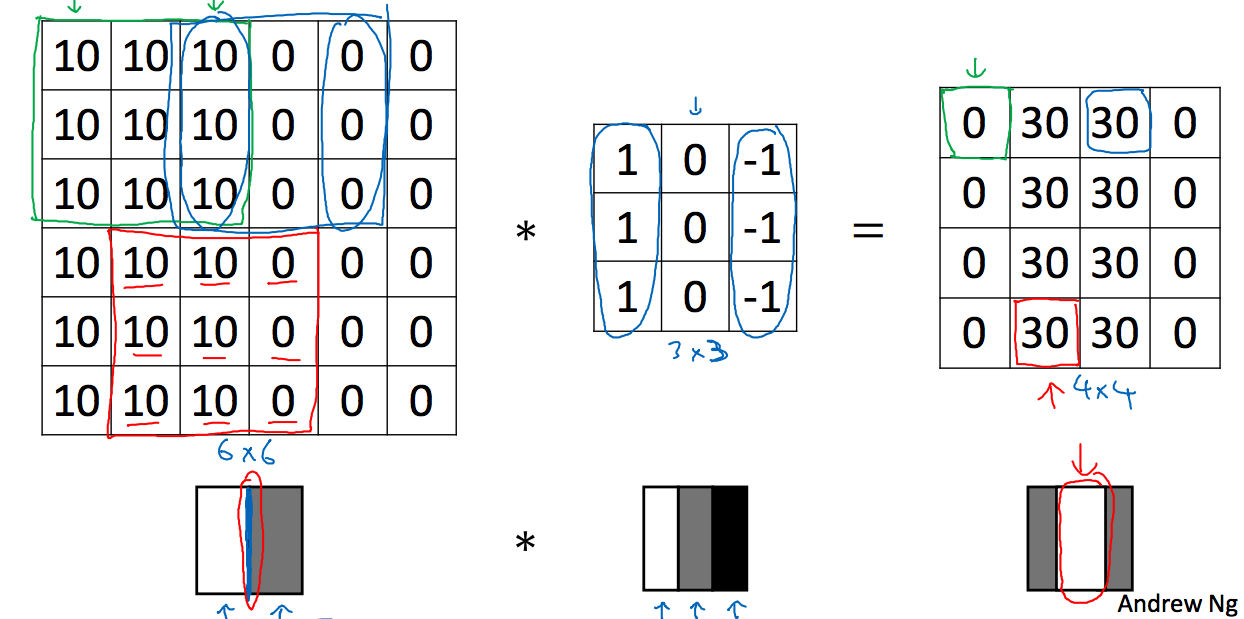
左边给出的图像矩阵可以看成是下图颜色矩阵,我们需要区分这个图像的垂直边缘线,使用的过滤矩阵如中间部分所示,卷积的结果就是右图所示,可以看到右图的中间部分有一条白线(虽然很粗,但是如果图像矩阵很大,这个结果很细了),这就是垂直边缘检测的结果。
1.3 更多边缘检测内容
如下图所示: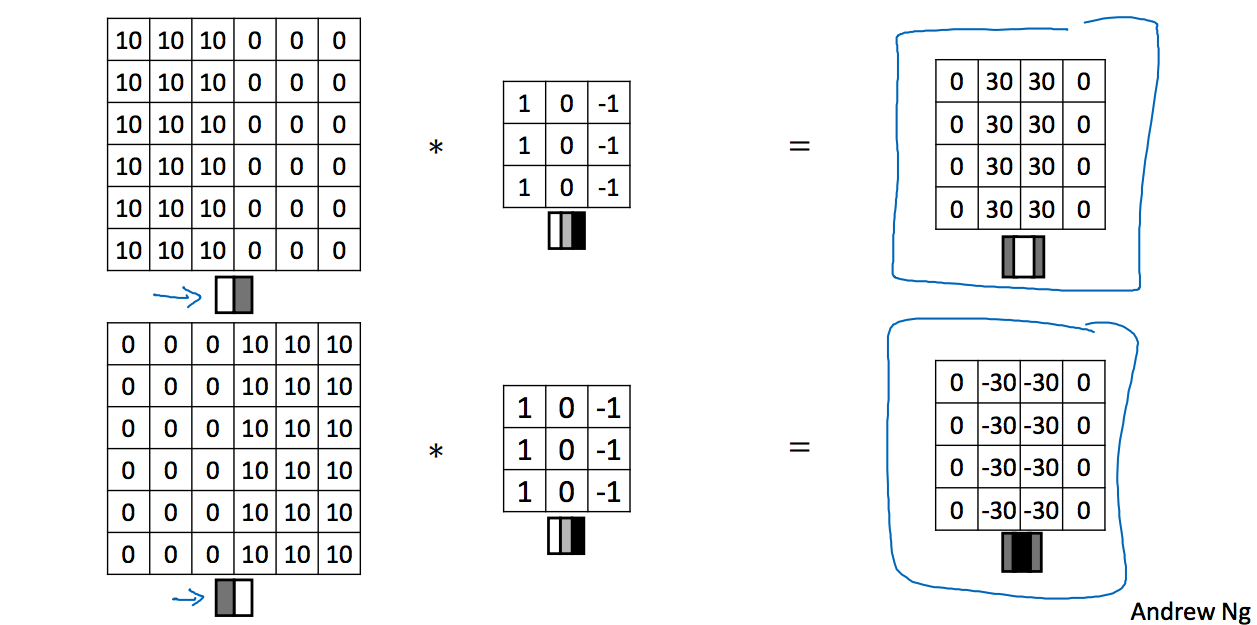
上面的卷积我们使用的是一张由亮变暗的图,卷积的结果是垂直边缘线非常的亮,但是如果使用一张下面的由暗变亮的图,卷积的结果的垂直边缘线非常暗。也就是说结果矩阵可以判断边缘线周边的颜色过渡方向,当然也可以将卷积的结果取绝对值,只了解边缘线即可。
上面的3x3的过滤器是检测垂直边缘线,当然变换一下过滤器,我们就可以检测水平边缘线。比如下图所示: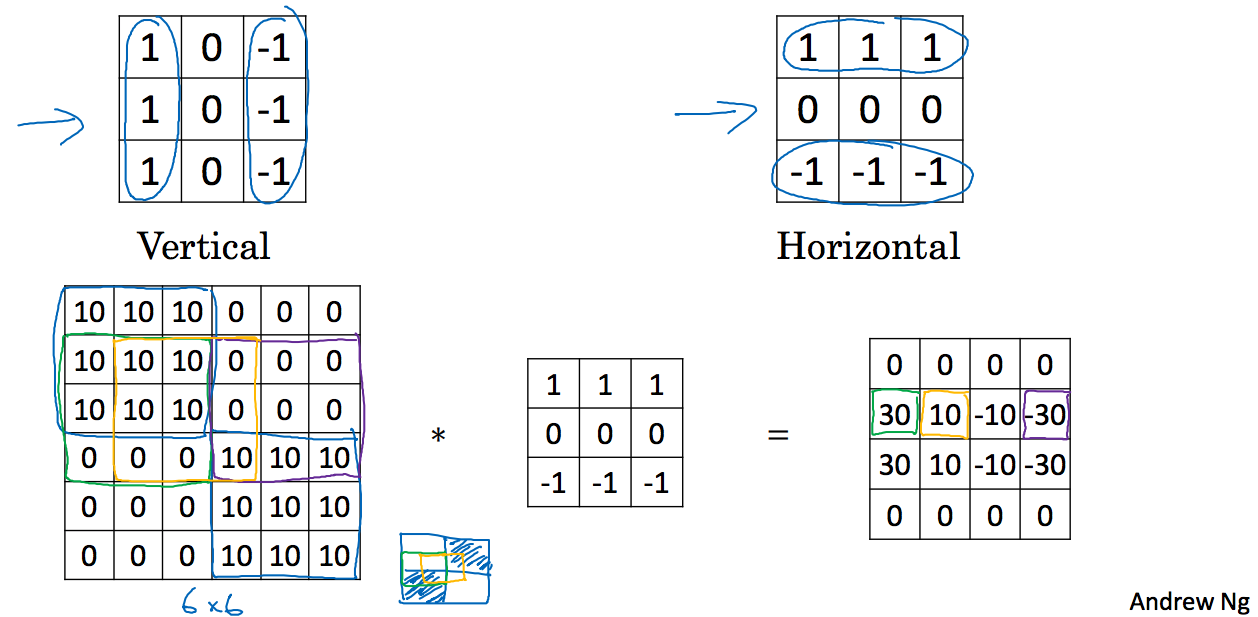
图片是一个6x6的矩阵,这张图的主对角线是暗色,副对角线是亮色,通过水平过滤器后的结果如右边,这里因为图片太小,所以出现的30比较少,如果图片大的话,就会有很多30,这样就可以看到一条30的亮水平线和一条-30的暗水平线。
从上面的结果我们不难发现过滤器决定了我们选取的边缘线,那么应该如何选取3x3的过滤器呢?下面会提到使用反向传播来得到过滤器。
1.4 Padding
我们知道前面讲到的过滤器对图像卷积有两个缺点,第一个缺点就是每次做卷积后都会让图像矩阵的维度变小,可能缩小到1x1,我们不希望每次识别边缘或其他特征的时候,让维度变小;第二个缺点就是,比如图像矩阵的左上角的像素点,只被一个过滤器求和,分配到结果矩阵中的一个位置,但是中间的像素点可能被很多过滤器求和分配到结果矩阵中的多个位置。这意味着丢掉了图像边缘位置的许多信息。解决这两个问题的方法是使用padding,我们将图像矩阵扩展,如下图所示: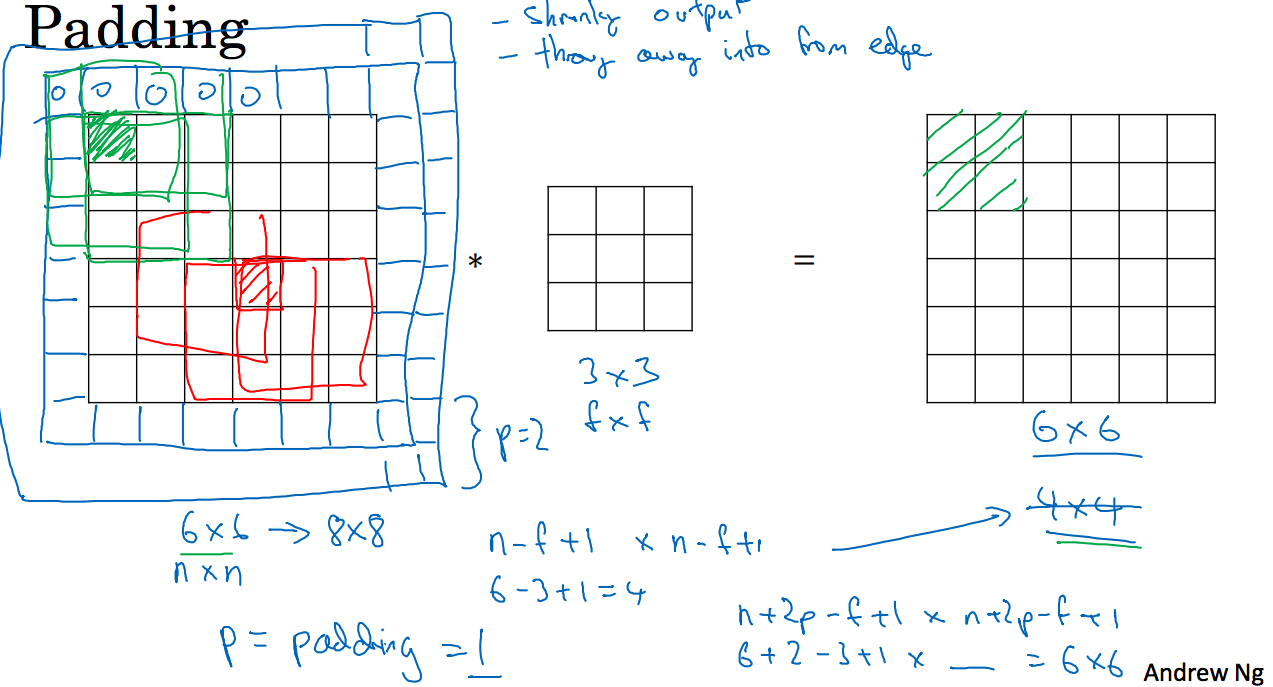
这里给出一个计算公式,图像矩阵的大小是nxn,过滤矩阵的大小是fxf,padding的大小是p,那么结果居中的大小为(n+2p-f+1)x(n+2p-f+1),如果让卷积后的结果不改变维度,那么需要满足2p-f+1=0。
1.5 卷积步长
这一部分就讲了如果将步长设置为2,该如何处理,以及卷积的含义。
这里记步长为s,那么上面的公式需要修正为:,这里需要注意的是,如果不能整除,就想下取整,也就是说如果过滤器越过图像矩阵的边界了,就不需要再计算了。
然后讲到实际的卷积是需要镜像,翻转的,如下图所示,但是深度学习中不需要这么做:
1.6 卷积中卷的体现
上面提到的图像矩阵都是黑白的,如果是RGB的呢,如下图所示: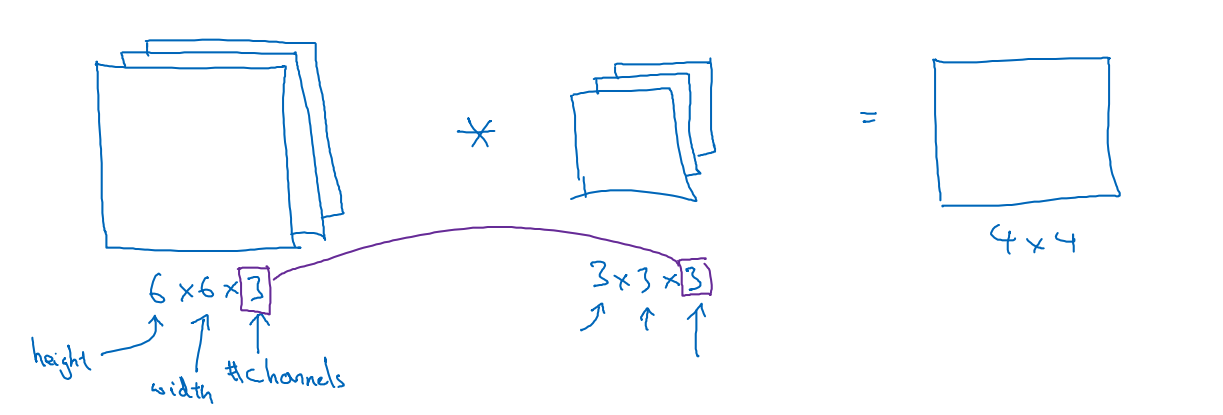
这里图像是一个6x6x3的矩阵,过滤器是3x3x3的矩阵(分别对应R,G,B),卷积后的结果是一个4x4的矩阵,也就是说结果矩阵中的每个元素都是由3x3x3的两个矩阵相乘求和得到的。
这里过滤器在检测边缘时,可以只检测红色的边缘线,那么只需要令R层为前面提到的二维矩阵形式即可,其他两层均为0,当然如果仅仅检测边缘,而不考虑颜色,可以让这三层都一样,即如下图所示:
我们知道结果矩阵是一个二维的,而我们给出的图像矩阵是3维的,那么怎么样让结果矩阵也是立体的呢,使用多个过滤器就可以了,如下图: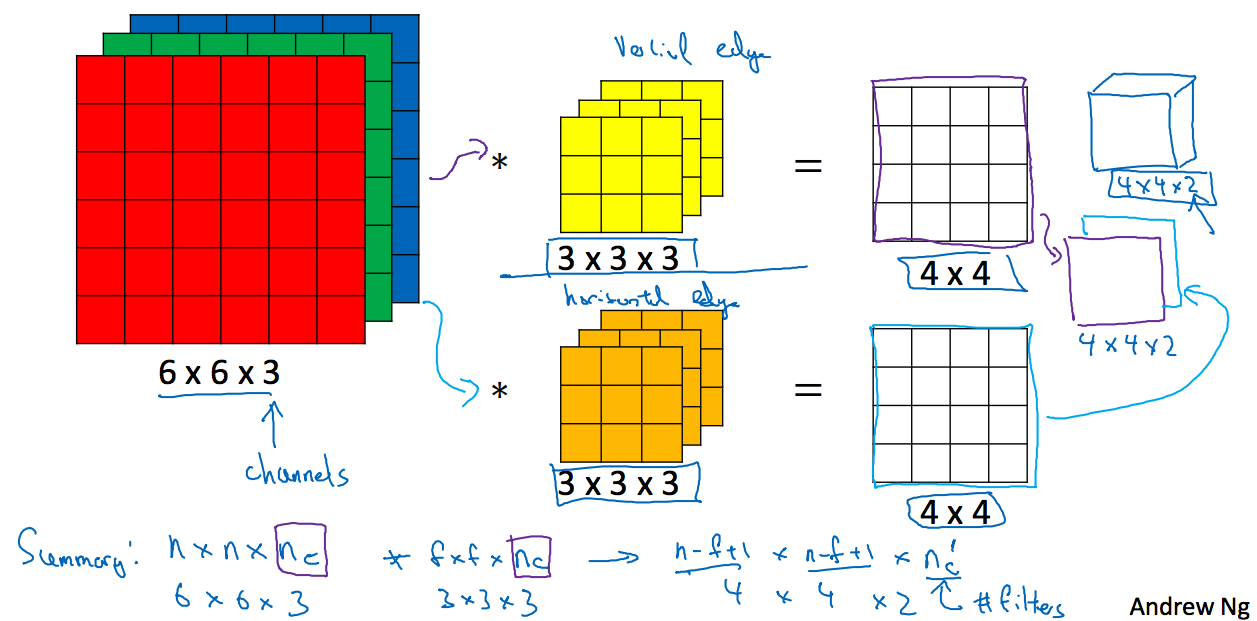
1.7 单层卷积网络
这一部分没什么好讲的,简单的对维度进行分析,如下图所示: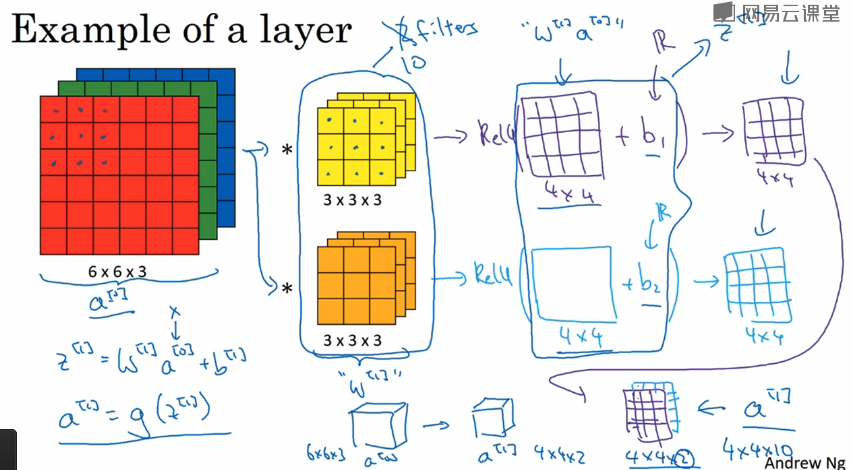
就说到通道数是由不同过滤器的个数决定的,对卷积后的结果需要加上偏差,然后进入到ReLU的激活函数,作为下一层的输入。
这里比如过滤器的个数是10个,大小为3x3x3,那么其参数个数为(27+1)x10=280个。后面讲到的是维度分析。。。
1.8 简单卷积网络示例
这一部分就讲了一个问题,就是下图部分:
首先是一张大小为39x39x3的图片矩阵,通过10个3x3x3的过滤器,步长为1,padding为0的卷积后,得到37x37x10的矩阵,这里结果矩阵的通道个数等于过滤器个数,37由前面的公式可以得到;然后通过20个5x5x10的过滤器矩阵(过滤器的通道个数等于输入矩阵的通道个数),步长为2,padding为0的卷积后,得到17x17x20的矩阵,继续通过40个5x5x20的过滤器,步长为2,padding为0的卷积后,得到7x7x40的矩阵,展开为1960个特征,然后通过softmax输出结果。
最后提到一个卷积网络包含卷积层,池化层,全连接层这三个部分。
1.9 池化层
池化层同样也有步长,但是计算上和卷积就不一样了,比如最大池化,如下图所示: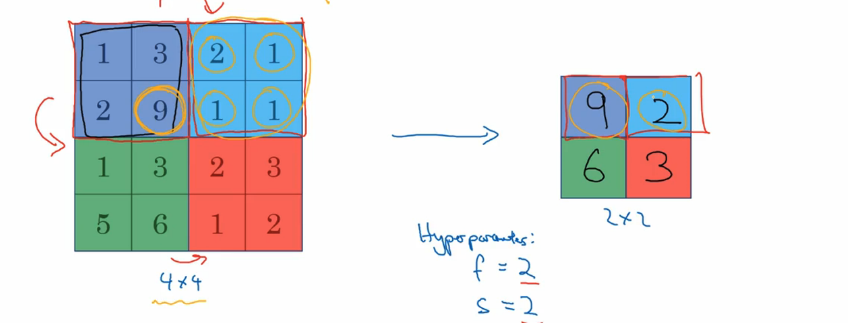
步长为2,过滤器矩阵为2x2,在2x2的区域里面选取最大的值就是最大池化,如上图,池化后的由4x4的矩阵变为2x2的矩阵。这一点同样可以使用上面的公式。除了最大池化外,还有平均池化,这里就是将选取的过滤矩阵对应的值求和在平均作为池化后的结果,如下图所示: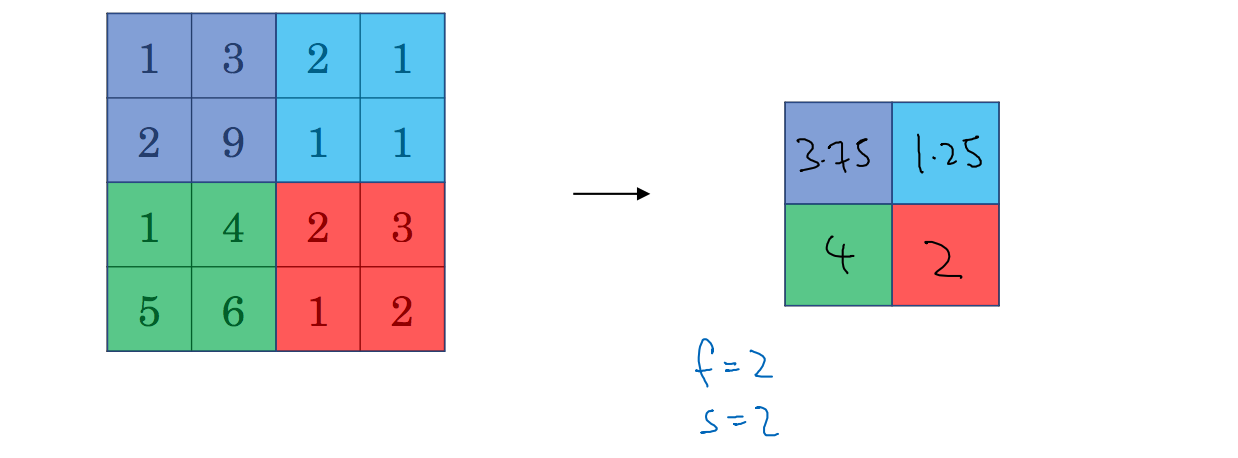
总结:池化一般有三个参数:过滤器大小,步长,最大池化或者平均池化。
1.10 卷积神经网络示例
这一节举了一个完整的卷积神经网络的过程,见下面这张图: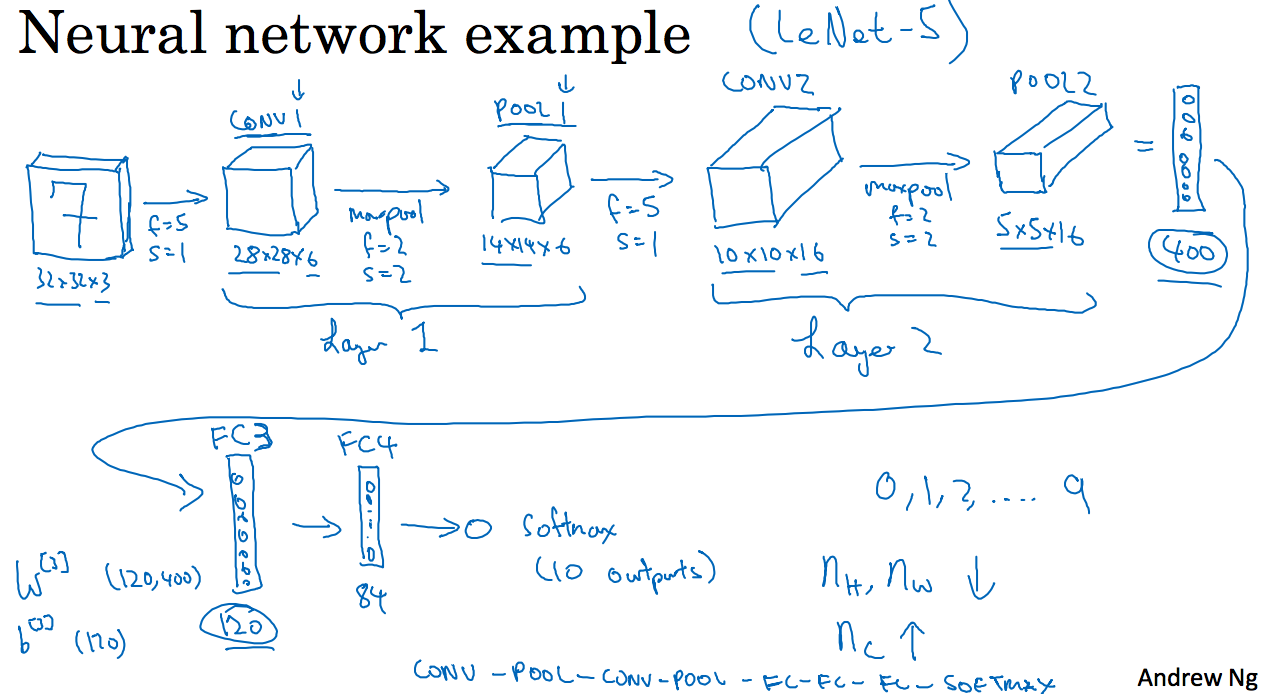
图像矩阵是一个32x32x3的矩阵,然后通过两个组合层,最后经过全连接层输出。其中组合层由卷积层和池化层组成。具体就不细说了。。。
1.11 为什么要使用卷积
使用卷积层和只用全连接层相比,卷积层的两个主要的优势在于参数共享和稀疏连接,如下图所示: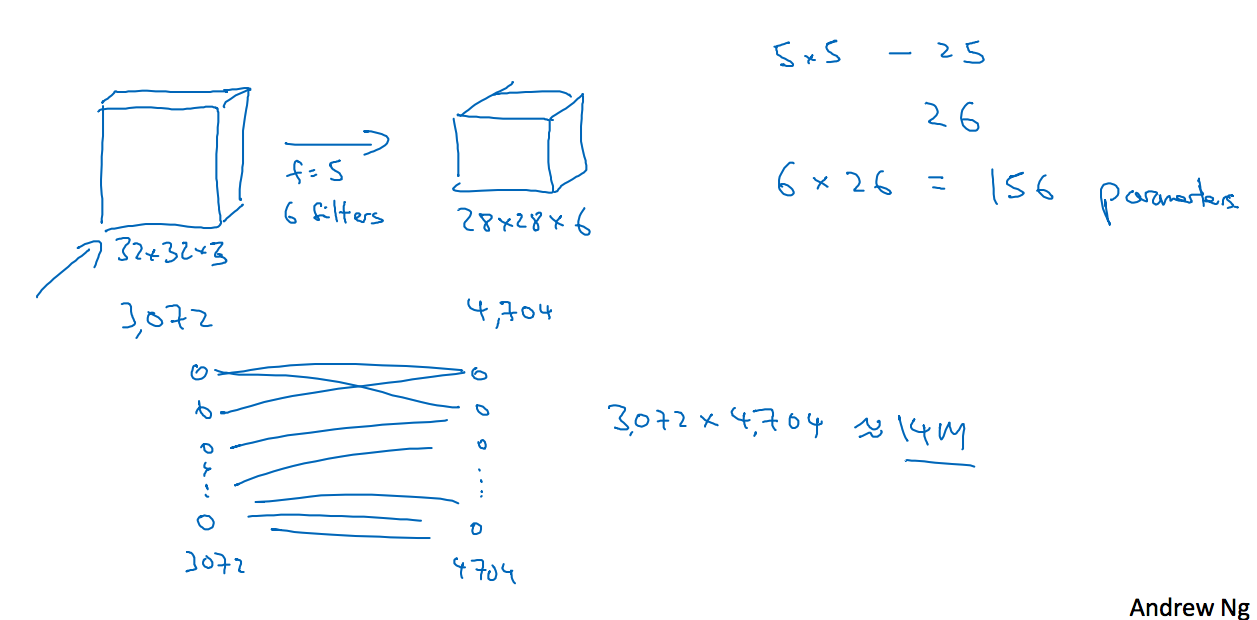
输入部分为32x32x3,一共3072个单元,第二层得到的矩阵是28x28x6,一共4704个单元,使用卷积层所需参数为(5x5+1)x6=156,但是使用全连接层就需要3072x4704个参数。
再来说参数共享,如下图所示: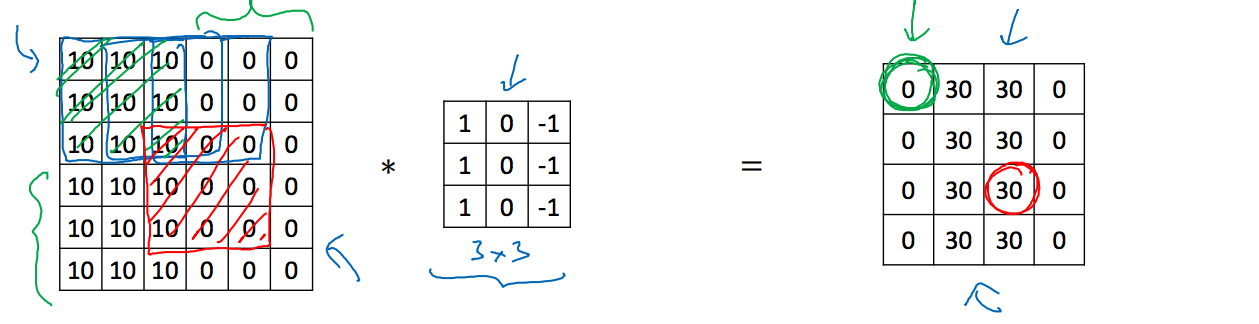
比如你用一个3x3的过滤器来检测垂直边缘,那么图片的左上角区域以及旁边的各个区域都可以使用这个3x3的过滤器,每个特征检测以及输出都可以在输入图片的不同区域中使用同样的参数,以便提取垂直边缘或其它特征。它不仅适用于边缘特征这样的低阶特征,同样适用于高阶特征,比如提取脸上的眼睛,及时减少了参数的个数,同样能提取一样多的输出。也就是说,比如一个垂直边缘检测器,用于检测图片左上角区域的特征,其参数也同样适合于检测图片右下角区域,因此,在计算图片左上角和右下角区域时,不需要添加其它检测器,同样能达到很好的效果。
上面提到的稀疏连接,这里再讲一下,比如结果矩阵中的单元0,只与输入矩阵的前9个值有关,而和其它的值没有关系。

