Deep Neural Networks

神经网络和深度学习[1-2]
神经网络和深度学习[1-3]
神经网络和深度学习[1-4]
改善深层神经网络：超参数调试、正则化以及优化【2-1】
改善深层神经网络：超参数调试、正则化以及优化【2-2】
改善深层神经网络：超参数调试、正则化以及优化【2-3】
结构化机器学习项目 3
Ng的深度学习视频笔记，长期更新

4.1 Deep L-layer Neural network

如下图所示，一个4层的神经网络，给出一些符号约定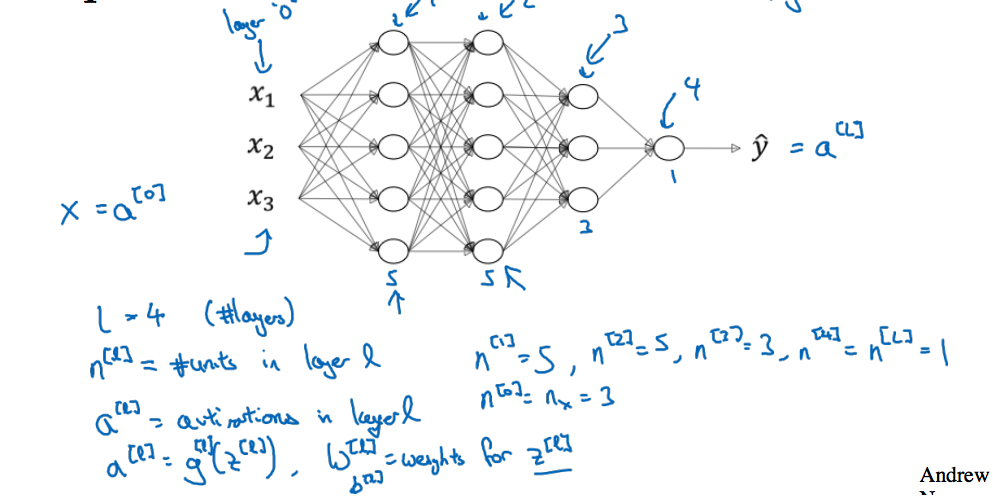

4.2 Forward Propagation in a Deep Network

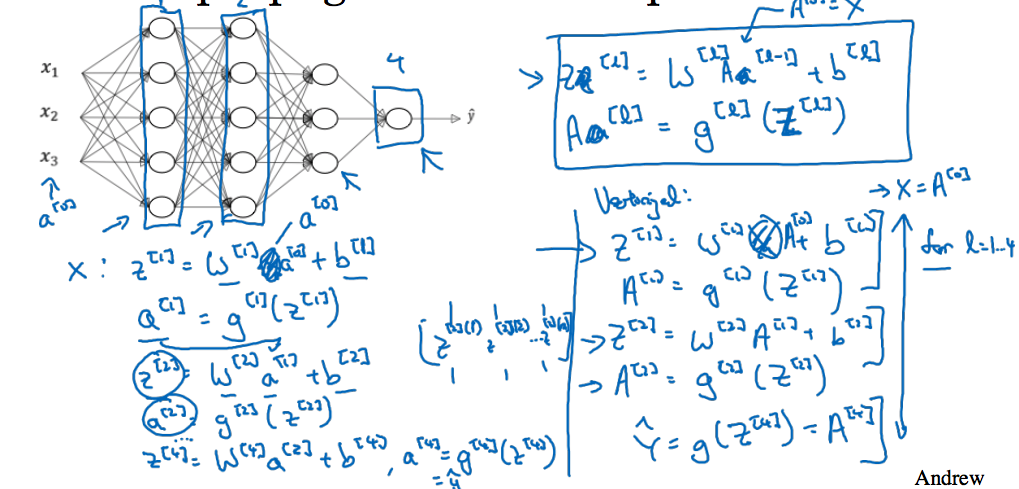
对于每一层的Z和A有如下公式：

$$Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]}\\ A^{[l]}=g^{[l]}(Z^{[l]})$$

4.3 Getting your matrix dimensions right

讲到了对于一个深层神经网络中各层参数及输出的维度，这里我之间有做过，就不罗列了

4.5 Building blocks of deep neural networks

继续上图，给出的是某一层的前向和反向的分析，在前向传播的过程中，传入$A^{[l-1]}$，输出$A^{[l]}$，这个过程需要计算出$Z^{[l]}$，才能得到$A^{[l]}$,而在反向传播中需要$Z^{[l]}$，因此需要将$Z^{[l]}$存储下来，供反向传播使用；反向传播是一个相反的过程，传入$dA^{[l]}$，输出$dA^{[l-1]}$，并计算$dW^{[l]},db^{[l]}$；这里为什么需要$Z^{[l]}$呢，因为求$dW^{[l]}$时，需要求解$dZ^{[l]}$，而求解$dZ^{[l]}$又要求解$\frac{dg^{[l]}(Z^{[l]})}{dZ^{[l]}}$，如果激活函数是$\sigma(x)$函数的话，该结果就是$\sigma(x)(1-\sigma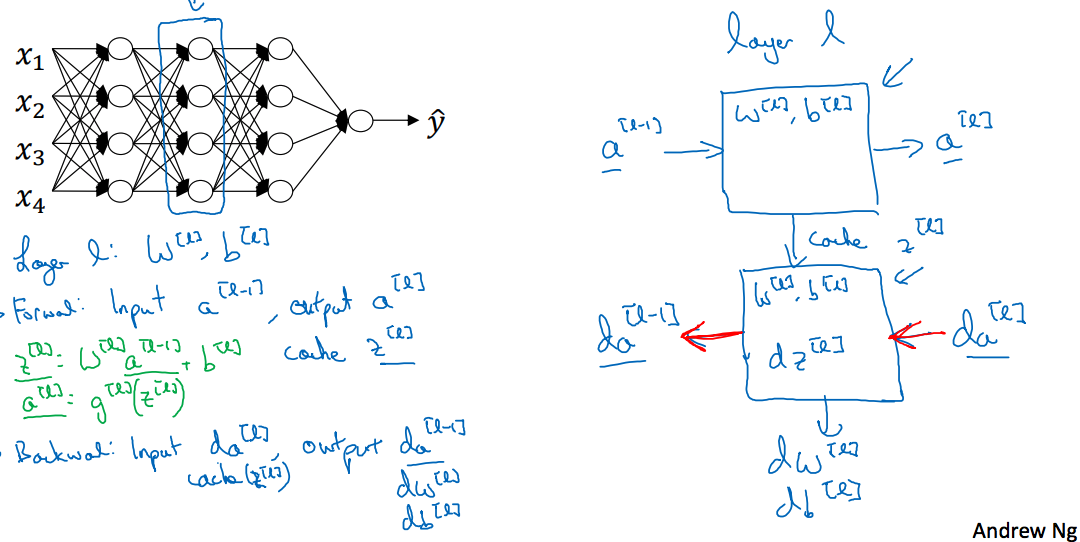(x))$，这里就要用到$Z^{[l]}$，避免重复计算。

下面这个是完整的神经网络过程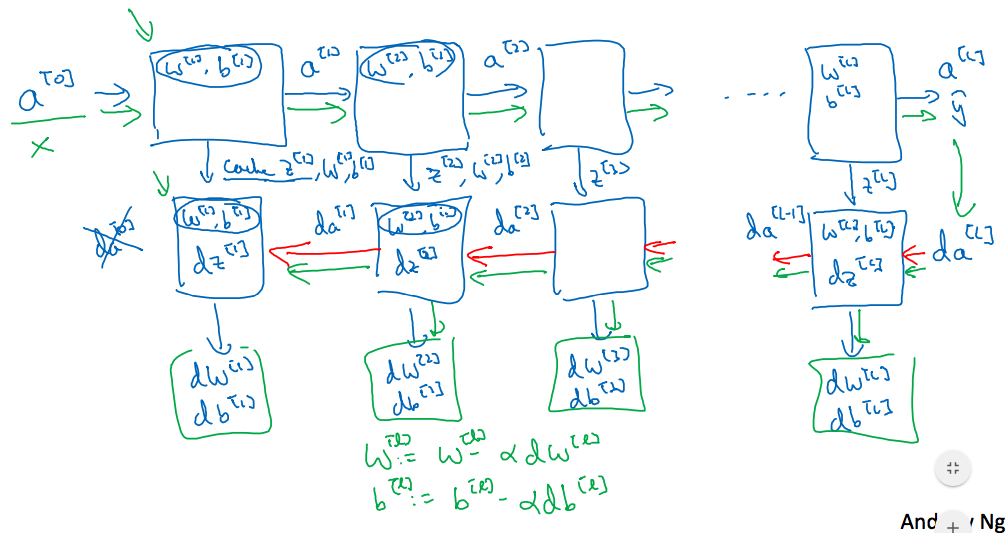

4.6 Forward and backward propagation

这节在讲上面的算法如何用向量表示及用代码实现，先上两张图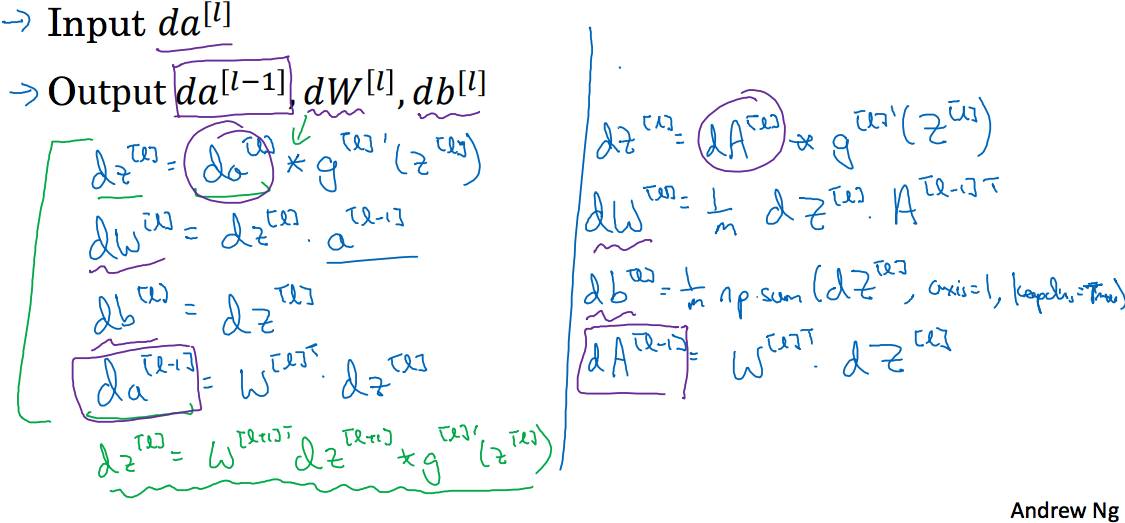


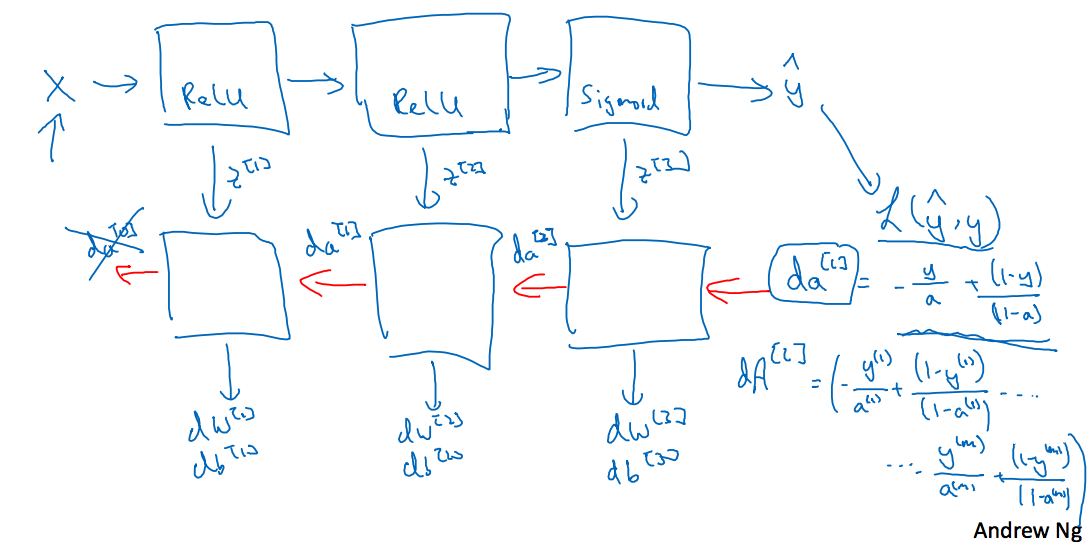
上面第一张图中有4组公式，也是我第三周的课程中想讲的，这里依次讲解，小写代表一个样本，大写代表有m个样本。

第一组公式：$dz^{[l]}=da^{[l]} \cdot g^{[l]'}(z^{[l]})$和$dZ^{[l]}=dA^{[l]} \cdot g^{[l]'}(Z^{[l]})$
这里Input为$da^{[l]}$已知，因为z的维度是$(n^{[l]},1)$，$g^{[l]'}(z^{[l]}$显然也是$(n^{[l]},1)$，a和z本来就是同维度的，只是使用了激活函数而已，这里就应该是简单的矩阵点乘；同理 A,Z。

第二组公式：$dW^{[l]}=dz^{[l]} \cdot a^{[l-1]}$和$dW^{[l]}=\frac{1}{m}dZ^{[l]} (A^{[l-1]})^{T}$
对于W，z而言，W的维度是$(n^{[l]},n^{[l-1]})$，$dz^{[l]}$的维度是$(n^{[l]},1)$，$a^{[l-1]}$的维度是$(n^{[l-1]},1)$，很显然就是将a转置就可以了；至于W和Z，这里无非是将z的维度变为$(n^{[l]},m)$，增加到m个样本，而A也变为$(n^{[l-1]},m)$，此处求解dW时就是将这些样本每一个作用的结果累计求和然后取平均的结果。

第三组公式：$db^{[l]}=dz^{[l]}$和$db^{[l]}=\frac{1}{m}np.sum(dZ^{[l]},axis=1,keepdims=True)$
db的维度是$(n^{[l]},1)$，和dz的维度一样，而dZ只是多个样本的结果，列变成了m，此时只需要对行进行求和即可。

第四组公式：$da^{[l-1]}=(W^{[l]})^{T} dz^{[l]}$和$dA^{[l-1]}=(W^{[l]})^{T} dZ^{[l]}$
其中$da^{[l-1]}$对应着$dz^{[l-1]}$，即维度为$(n^{[l-1]},1)$，$W^{[l]}$的维度为$(n^{[l]},n^{[l-1]})$，$dz^{[l]}$的维度为$(n^{[l]},1)$，这样就是要$W^{[l]}$转置即可；对应的如果样本变为m后，$dA^{[l-1]}$的维度为$(n^{[l-1]},m)$，$dZ^{[l]}$的维度为$(n^{[l]},m)$，这样和之前没有什么变化。

下面就用python实现一个深层神经网络的一般模型

"""
该程序为自己听完视频后写出来的，所以有很多不规范的地方，但是我仍然保留下来，因为这是没有修饰的代码，写的更直观，更本质

X为n行（特征）m列（样本个数）
Y为1行m列（样本标签）
nh为隐藏层数组，其中nh[i]表示的是第i+1层神经元的个数
n_y=1,输出层为一个神经元
"""
def forward_backward_code(X,Y,nh,n_y,num_iter,learning_rate):
    n_x,m=X.shape
    W=list()#这里用W表示全部的参数集合，即W1,W2,W3,...
    b=list()#同上
    W.append(0)#这里为了和A，Z保持一致，添加的值没有用
    b.append(0)
    #参数初始化
    pre_n=n_x
    for i in range(len(nh)):
        sta_n=nh[i]
        W.append(np.random.randn(sta_n,pre_n))#用标准正太分布来初始化W
        b.append(np.zeros((sta_n,1)))#用0初始化b
        pre_n=sta_n
    #这里还需要加上最后一层，输出层
    W.append(np.random.randn(pre_n,n_y))
    b.append(np.zeros((n_y,1)))


    for i in num_iter:
        #前向传播，隐藏层全部用tanh函数
        Z = list()
        A = list()
        A.append(X)  # 将X作为A[0]
        Z.append(0)  # 这里添加任意值，只是为了让A和Z对齐
        for j in range(1,len(W-1)):
            Z.append(np.dot(W[j],A[j])+b[j])
            A.append(np.tanh(Z[j]))
        #最后一层用Sigmoid函数
        j+=1
        Z.append(np.dot(W[j],A[j])+b[j])
        A.append(sigmoid(Z[j]))


        #反向传播
        dZ=list()
        dW=list()
        db=list()
        dA=list()
        j=len(A)-1
        #最后一层,这里是Sigmoid函数
        dZ.append(A[j]-Y)
        dW.append(1/m*np.dot(dZ[0],A[j-1].T))
        db.append(1/m*np.sum(dZ[0],axis=1,keepdims=True))
        dA.append(np.dot(W[j].T,dZ[0]))
        #其它层
        j-=1
        while j>0:
            dZ.insert(np.multiply(dA[0],1-np.tanh(Z[j])),0)
            dW.insert(1/m*np.dot(dZ[0],A[j-1].T),0)
            db.insert(1/m*np.sum(dZ[0],axis=1,keepdims=True),0)
            dA.insert(np.dot(W[j].T,dZ[0]),0)
            j-=1;

        #更新参数
        for j in range(1,len(W)):
            W[j]=W[j]-learning_rate*dW[j];
            b[j]=b[j]-learning_rate*db[j];

大作业

搭建一个多层的神经网络，然后对cat进行预测。
作业地址：
Building your Deep Neural Network - Step by Step v5
Deep Neural Network - Application v3

分为初始化函数，前向函数，成本函数，反向函数，参数更新这几个部分。
初始化

# GRADED FUNCTION: initialize_parameters_deep

def initialize_parameters_deep(layer_dims):
    """
    Arguments:
    layer_dims -- python array (list) containing the dimensions of each layer in our network
    
    Returns:
    parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
                    Wl -- weight matrix of shape (layer_dims[l], layer_dims[l-1])
                    bl -- bias vector of shape (layer_dims[l], 1)
    """
    
    np.random.seed(3)
    parameters = {}
    L = len(layer_dims)            # number of layers in the network

    for l in range(1, L):
        ### START CODE HERE ### (≈ 2 lines of code)
        parameters['W' + str(l)] = np.random.randn(layer_dims[l],layer_dims[l-1])*0.01
        parameters['b' + str(l)] = np.zeros((layer_dims[l],1))
        ### END CODE HERE ###
        
        assert(parameters['W' + str(l)].shape == (layer_dims[l], layer_dims[l-1]))
        assert(parameters['b' + str(l)].shape == (layer_dims[l], 1))

        
    return parameters

前向传播

def linear_activation_forward(A_prev, W, b, activation):
    """
    Implement the forward propagation for the LINEAR->ACTIVATION layer

    Arguments:
    A_prev -- activations from previous layer (or input data): (size of previous layer, number of examples)
    W -- weights matrix: numpy array of shape (size of current layer, size of previous layer)
    b -- bias vector, numpy array of shape (size of the current layer, 1)
    activation -- the activation to be used in this layer, stored as a text string: "sigmoid" or "relu"

    Returns:
    A -- the output of the activation function, also called the post-activation value 
    cache -- a python dictionary containing "linear_cache" and "activation_cache";
             stored for computing the backward pass efficiently
    """
    
    if activation == "sigmoid":
        # Inputs: "A_prev, W, b". Outputs: "A, activation_cache".
        ### START CODE HERE ### (≈ 2 lines of code)
        Z, linear_cache = linear_forward(A_prev, W, b)
        A, activation_cache = sigmoid(Z)
        ### END CODE HERE ###
    
    elif activation == "relu":
        # Inputs: "A_prev, W, b". Outputs: "A, activation_cache".
        ### START CODE HERE ### (≈ 2 lines of code)
        Z, linear_cache = linear_forward(A_prev, W, b)
        A, activation_cache = relu(Z)
        ### END CODE HERE ###
    
    assert (A.shape == (W.shape[0], A_prev.shape[1]))
    cache = (linear_cache, activation_cache)

    return A, cache

# GRADED FUNCTION: L_model_forward

def L_model_forward(X, parameters):
    """
    Implement forward propagation for the [LINEAR->RELU]*(L-1)->LINEAR->SIGMOID computation
    
    Arguments:
    X -- data, numpy array of shape (input size, number of examples)
    parameters -- output of initialize_parameters_deep()
    
    Returns:
    AL -- last post-activation value
    caches -- list of caches containing:
                every cache of linear_relu_forward() (there are L-1 of them, indexed from 0 to L-2)
                the cache of linear_sigmoid_forward() (there is one, indexed L-1)
    """

    caches = []
    A = X
    L = len(parameters) // 2                  # number of layers in the neural network
    
    # Implement [LINEAR -> RELU]*(L-1). Add "cache" to the "caches" list.
    for l in range(1, L):
        A_prev = A 
        ### START CODE HERE ### (≈ 2 lines of code)
        A, cache = linear_activation_forward(A_prev,parameters['W'+str(l)],parameters['b'+str(l)],'relu')
        
        ### END CODE HERE ###
    
    # Implement LINEAR -> SIGMOID. Add "cache" to the "caches" list.
    ### START CODE HERE ### (≈ 2 lines of code)
    AL, cache = linear_activation_forward(A_prev,parameters['W'+str(L)],parameters['b'+str(L)],'sigmoid')

    ### END CODE HERE ###
    
    assert(AL.shape == (1,X.shape[1]))
            
    return AL, caches

成本函数

def compute_cost(AL, Y):
    """
    Implement the cost function defined by equation (7).

    Arguments:
    AL -- probability vector corresponding to your label predictions, shape (1, number of examples)
    Y -- true "label" vector (for example: containing 0 if non-cat, 1 if cat), shape (1, number of examples)

    Returns:
    cost -- cross-entropy cost
    """
    
    m = Y.shape[1]

    # Compute loss from aL and y.
    ### START CODE HERE ### (≈ 1 lines of code)
    cost = 1/m*np.sum(np.multiply(Y,np.log(AL))+np.multiply((1-Y),np.log(1-AL)))
    ### END CODE HERE ###
    
    cost = np.squeeze(cost)      # To make sure your cost's shape is what we expect (e.g. this turns [[17]] into 17).
    assert(cost.shape == ())
    
    return cost

反向传播

def linear_activation_backward(dA, cache, activation):
    """
    Implement the backward propagation for the LINEAR->ACTIVATION layer.
    
    Arguments:
    dA -- post-activation gradient for current layer l 
    cache -- tuple of values (linear_cache, activation_cache) we store for computing backward propagation efficiently
    activation -- the activation to be used in this layer, stored as a text string: "sigmoid" or "relu"
    
    Returns:
    dA_prev -- Gradient of the cost with respect to the activation (of the previous layer l-1), same shape as A_prev
    dW -- Gradient of the cost with respect to W (current layer l), same shape as W
    db -- Gradient of the cost with respect to b (current layer l), same shape as b
    """
    linear_cache, activation_cache = cache
    
    if activation == "relu":
        ### START CODE HERE ### (≈ 2 lines of code)
        dZ = relu_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache)
        ### END CODE HERE ###
        
    elif activation == "sigmoid":
        ### START CODE HERE ### (≈ 2 lines of code)
        dZ = sigmoid_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache)
        ### END CODE HERE ###
    
    return dA_prev, dW, db


def L_model_backward(AL, Y, caches):
    """
    Implement the backward propagation for the [LINEAR->RELU] * (L-1) -> LINEAR -> SIGMOID group
    
    Arguments:
    AL -- probability vector, output of the forward propagation (L_model_forward())
    Y -- true "label" vector (containing 0 if non-cat, 1 if cat)
    caches -- list of caches containing:
                every cache of linear_activation_forward() with "relu" (it's caches[l], for l in range(L-1) i.e l = 0...L-2)
                the cache of linear_activation_forward() with "sigmoid" (it's caches[L-1])
    
    Returns:
    grads -- A dictionary with the gradients
             grads["dA" + str(l)] = ... 
             grads["dW" + str(l)] = ...
             grads["db" + str(l)] = ... 
    """
    grads = {}
    L = len(caches) # the number of layers
    m = AL.shape[1]
    Y = Y.reshape(AL.shape) # after this line, Y is the same shape as AL
    
    # Initializing the backpropagation
    ### START CODE HERE ### (1 line of code)
    dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
    ### END CODE HERE ###
    
    # Lth layer (SIGMOID -> LINEAR) gradients. Inputs: "AL, Y, caches". Outputs: "grads["dAL"], grads["dWL"], grads["dbL"]
    ### START CODE HERE ### (approx. 2 lines)
    current_cache = caches[-1]
    grads["dA" + str(L)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL, current_cache, 'sigmoid')
    ### END CODE HERE ###
    
    for l in reversed(range(L-1)):
        # lth layer: (RELU -> LINEAR) gradients.
        # Inputs: "grads["dA" + str(l + 2)], caches". Outputs: "grads["dA" + str(l + 1)] , grads["dW" + str(l + 1)] , grads["db" + str(l + 1)] 
        ### START CODE HERE ### (approx. 5 lines)
        current_cache = caches[l]
        dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads['dA'+str(l+2)], current_cache, 'relu')
        grads["dA" + str(l + 1)] = dA_prev_temp
        grads["dW" + str(l + 1)] = dW_temp
        grads["db" + str(l + 1)] = db_temp
        ### END CODE HERE ###

    return grads

参数更新

def update_parameters(parameters, grads, learning_rate):
    """
    Update parameters using gradient descent
    
    Arguments:
    parameters -- python dictionary containing your parameters 
    grads -- python dictionary containing your gradients, output of L_model_backward
    
    Returns:
    parameters -- python dictionary containing your updated parameters 
                  parameters["W" + str(l)] = ... 
                  parameters["b" + str(l)] = ...
    """
    
    L = len(parameters) // 2 # number of layers in the neural network

    # Update rule for each parameter. Use a for loop.
    ### START CODE HERE ### (≈ 3 lines of code)
    for l in range(L):
        parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * grads["dW" + str(l+1)]
        parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * grads["db" + str(l+1)]
    ### END CODE HERE ###
    return parameters

详细请参考作业地址