机器学习中的数学知识

复习过程中遇到的一些机器学习中与数学相关的知识，总结于此

线性代数中的基础知识

设A是n阶矩阵，如果数$\lambda$和n维非零列向量x式关系式

$$Ax=\lambda x$$

成立，那么，这样的数$\lambda$称为矩阵A的特征值，非零向量x称为A的对应于特征值$\lambda$的特征向量

特征值分解

对于一个方阵，可以将其表现为如下形式：

$$Av=\lambda v$$

可以将A分解为如下形式：

$$A=Q\sum Q^{-1}$$

特征值分解后，分解得到的$\sum$矩阵是一个对角阵，里面的特征值是由大到小排列的，这些特征值所对应的前N个特征向量，对应了这个矩阵最重要的N各变化方向。利用这前N个变化方向就可以近似这个矩阵。
特征值分解最大的局限就是变换矩阵必须是方阵

SVD分解

奇异值分解是一个能适合任意矩阵的一种分解方式：

$$A=U\sum V^{T}$$

假设A是一个N M的矩阵，那么得到的U是一个N N的方阵（里面的向量是正交的，U里面的向量称为左奇异向量），Σ是一个N M的矩阵（除了对角线的元素都是0，对角线上的元素称为奇异值），V’(V的转置)是一个N N的矩阵，里面的向量也是正交的，V里面的向量称为右奇异向量）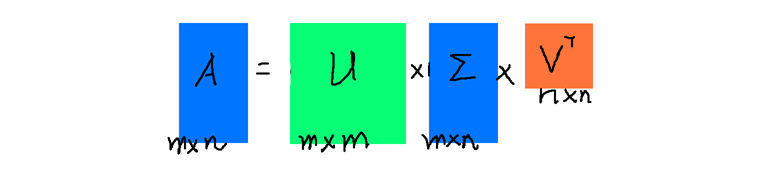

关于SVD求解，比如如下：

$$(A^TA)v_i=\lambda_iv_i\\ 奇异值=\sqrt(\lambda_i)$$

参考

1. 同济大学《线性代数》第五版
2. 强大的矩阵奇异值分解及其应用