神经网络与梯度更新方面知识总结

面试过程中问到的一些深度学习中的东西总结。。。

激活函数

sigmoid

$$\sigma (x)=\frac{1}{1+exp(-x)}\\ \sigma^{'}(x)=\sigma(x)(1-\sigma(x))$$

sigmoid函数具有一切基本激活函数该有的功能

tanh

$$\tanh(x)=\frac{exp(x)-exp(-x)}{exp(x)+exp(-x)}=2\sigma(2x)-1\\ \tanh^{'}(x)=1-\tanh^{2}(x)$$

tanh就是变换后的sigmoid
tanh的优点：

• 在实践中被发现可以更快的收敛(因为tanh是0中心对称的，在训练过程中梯度方向可能会有正有负，这样对比非0均值而言更容易收敛)
• 梯度计算成本少(这个优点不太懂，对比与sigmoid吗？？？)

ReLU的反向传播：不可导的地方用分段函数表示
ReLU主要用在计算机视觉方面
ReLU的优点：

• 解决了梯度消失的问题(我看有提到解决梯度爆炸问题，这个我不太清楚，难道是左半部分梯度等于0，就解决的梯度爆炸吗？)
• 计算方便，计算速度快，加速网络训练

ReLU的缺点：

• 输出不是以0为中心的(这一点，在sigmoid和tanh对比的时候提到过)
• 如果梯度更新的过程中神经元的值小于0，ReLU的结果就是0，导致神经元死亡(通过降低学习率来解决)

leakrelu
leakrelu就是为了解决relu的0区间带来的影响，其数学表达为：

$$leakrelu=\begin{equation} f(x)= \begin{cases} x, & {x\gt 0} \\\\ x*k, & {x\leq 0} \end{cases} \end{equation}$$

其中k是leak系数，一般选择0.1或者0.2，或者通过学习而来
leakrelu解决了0区间带来的影响，而且包含了relu的所有优点

梯度消失与梯度爆炸

发生在梯度更新的过程中，对于每层的求导而言，都会有一个W参数和激活函数的导数相乘的信息，那么如果有很多层的话，就会有多个这样的信息相乘，如果W中对应的值小于1，就会导致最后的结果趋于0（梯度消失），激活函数的导数值也是同样的，反之，如果他们的乘积大于1，相对的就会出现梯度爆炸
梯度消失的解决方案：

• 改用其它激活函数：sigmoid激活函数导数的最大值是1/4，tanh导师最大值为1，但是relu正半轴导数恒等于1
• BN：在线性值y传入到激活函数前先通过一个BN的归一化，就是通过对每一层的输出做scale和shift的方法，通过一定的规范化手段，把每层神经网络任意神经元这个输入值的分布强行拉回到接近均值为0方差为1的标准正太分布，即严重偏离的分布强制拉回比较标准的分布，这样使得激活输入值落在非线性函数对输入比较敏感的区域，这样输入的小变化就会导致损失函数较大的变化，使得让梯度变大，避免梯度消失问题产生，而且梯度变大意味着学习收敛速度快，能大大加快训练速度。(此处有疑问：BN将传入到激活函数的值归一为均值近似为0，那么岂不是传入ReLU后有一半的值是0？？？[见数据预处理方法详解中对BN的解释])
• 残差网络
• LSTM

梯度爆炸的解决方案：

• 梯度剪切：设定梯度阈值，将梯度限定到该阈值之内
• 权重正则化：L1和L2正则，实质上Dropout也是(其实现就是不让模型过分依赖某些神经核，即降低该神经核对应的权重)
• BN
• 残差网络
• LSTM

CNN

卷积
卷积核：局部性，即它只关注局部特征，局部的程度决定了卷积核的大小
池化
池化的本质是采样，即压缩特征
其意义主要有两点：

1. 减少参数
2. 增强鲁棒性(可以从采样的角度理解，具体参见1)

关于池化层的反向传播：

1. mean pooling
   把某个元素的梯度等分为n份分配给前一层，和其前向计算过程相同，如下图：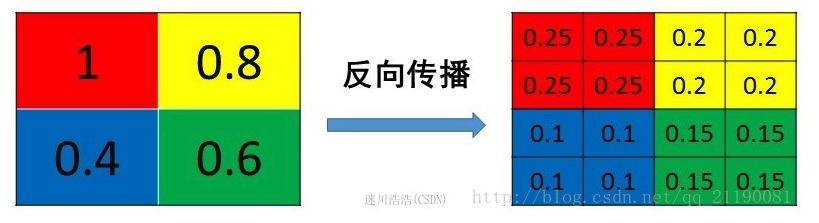
   
2. max pooling
   反向传播中只有前向传播过来的位置有值，其他位置为0，如下图：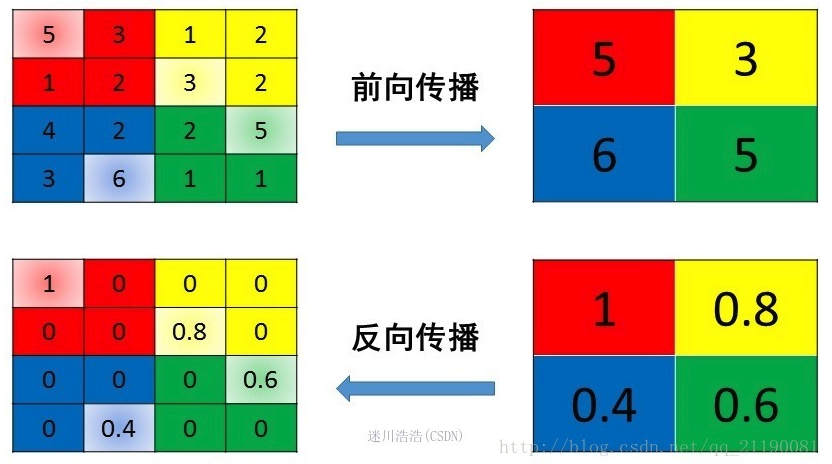
   

RNN，LSTM，GRU中

RNN这一部分我主要想提一下梯度消失的问题：
RNN中一层中共用一个参数W，对于一个普通的RNN网络如下：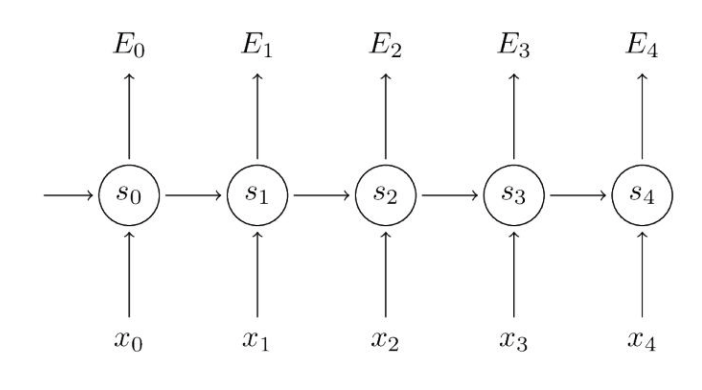

给出RNN的基本公式，定义损失为交叉损失函数：

$$s_{t}=f(Ux_{t}+Ws_{t-1}) \\ \hat{y_{t}}=softmax(Vs_{t})\\ E_{t}(y_{t},\hat{y_{t}})=-y_{t}log\hat{y_{t}}\\ E(y,\hat{y})=\sum_{t}^{}{E_{t}(y_{t},\hat{y_{t}})}=-\sum_{t}^{}{y_{t}log\hat{y_{t}}}$$

对W进行求导，因为每个时间节点都在使用W，因此是一个求和的过程：

$$\frac{\partial E}{\partial W}=\sum_{t}^{}{\frac{\partial E_{t}}{\partial W}}$$

这里对t时刻的梯度分析：

$$\frac{\partial E_t}{\partial W}=\sum_{k=1}^t\frac{\partial E_t}{\partial y_t}\frac{\partial y_t}{\partial s_t}\frac{\partial s_t}{\partial s_k}\frac{\partial s_k}{\partial W}\\ \frac{\partial s_t}{\partial s_k}=\prod_{j=k+1}^t\frac{\partial s_j}{\partial s_{j-1}}$$

这里的梯度求和的过程是这样的，比如对t时刻的梯度，除了受t时刻的输入影响外，还会受到t-1时刻，t-2时刻，… 等的影响，这里理解为长依赖，这正是RNN的优势所在，但是随着t的增加，越往前的时刻的输入对t的影响就越小，因为其对应的梯度值连乘的结果会严重受激活函数的导数与W乘积的影响，这样就掩盖了RNN的优势。

LSTM和GRU就解决了这个问题，反向传播如上所示，其内部结构之前已经烂熟于心，这里就不叙述了。

LSTM中为什么使用sigmoid和tanh，为什么不使用ReLU？
这里使用sigmoid可以理解为百分比的概念，而为什么使用tanh而不使用ReLU呢，因为LSTM的网络一般不会很深，而且LSTM解决了梯度消失的问题，不需要再使用ReLU了，不过当网络很深时，就会出现梯度消失的问题，可能需要使用ReLU。
为什么LSTM中要使用tanh：
The main problem in RNN is the vanishing gradient problem. Also, to keep the gradient in the linear region of the activation function, we need a function whose second derivative can sustain for a long range before going to zero.
Tanh is a good function with the above properties.
[不懂，和二阶导有啥关系？？？]

梯度下降与牛顿法

梯度下降

$$\theta_j=\theta_j-\alpha \frac{\partial J(\theta)}{\partial \theta_j}$$

梯度下降法利用的是切线的斜率
牛顿法
假设损失函数$J(\theta)$具有二阶连续偏导数，若第k次迭代值为$x^{(k)}$（初始化任意一个值），则可将$f(x)$在$x^{(k)}$附近进行二阶泰勒展开：

$$f(x)=f(x^{k})+g_{k}^{T}(x-x^{(k)})+\frac{1}{2}(x-x^{(k)})^{T}H(x^{(k)})(x-x^{(k)})$$

其中$g_k$为f(x)的梯度向量在$x^{(k)}$的值，$H(x^{(k)})$是f(x)的二阶梯度矩阵(海赛矩阵)

$$H(x)=\bigg[\frac{\partial^2 f}{\partial x_i \partial x_j}\bigg]_{n\times n}$$

对损失函数求导：

n问

1. lstm网络参数数量计算
2. lstm公式推导，前向传播公式
3. bp推导
4. cnn的卷积操作，cnn过滤器个数选择

参考

1.如何理解卷积神经网络中的卷积和池化
2.神经网络训练中的梯度消失和梯度爆炸
3.详解深度学习中的梯度消失，爆炸原因及解决方法
4.深度学习笔记(3)—-CNN中一些特殊环节的反向传播
5.CS224n Lecture Notes: Part V
6.LSTM question
7.CS224n Lecture Notes: Part III
8.What is the intuition of using tanh in LSTM
9.