主要学习资料是cs224n的notes和Michael Collins的notes,和宗成庆的统计自然语言处理,这里并不是一个完整的翻译笔记,而是在阅读的过程中对其中不懂的东西的一些解释,以及避免遗忘做的一些笔记,当然初入NLP,难免对一些知识理解不透或者有所偏差。
Weaknesses of PCFGs as Parsing Models
这一章是对上一章的优化,PCFGs主要有两个关键的弱点,第一个是缺乏对词汇信息的敏感度,第二个是缺乏对结构的偏好,第一个问题是我们使用lexicalized PCFGs的根本原因。
比如下面两棵 parse tree: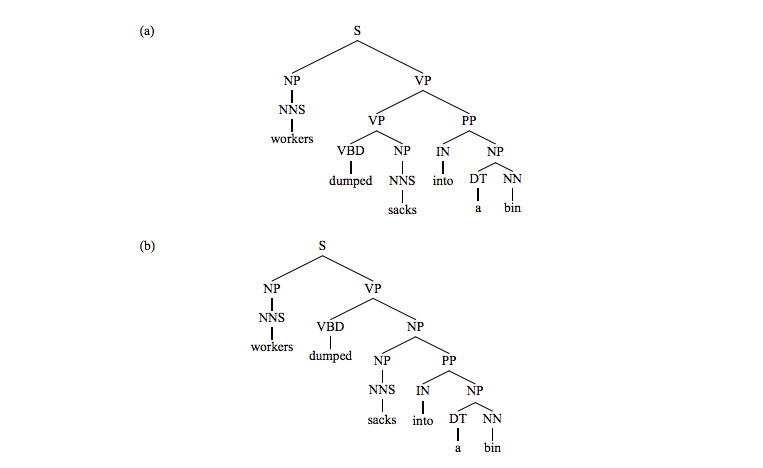
使用PCFGs来计算两棵树的概率:
可以发现选择那棵树完全取决于和的大小,也就是说统计语料库中和的个数,那个更多,就选择那棵树,和词汇没有一点关系;但是如果PP是和介词into一起,统计的结果是VP PP出现的次数是NP PP的9倍;而如果介词是of,统计的结果是NP PP出现的次数是VP PP的100倍,这就说明了PP中的词汇是有一定作用的。
第二个问题是缺乏结构偏好,比如下面这两棵parse tree: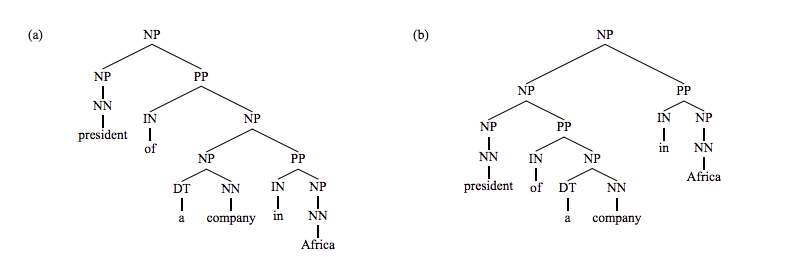
使用PCFGs计算的结果是一样的,无法区分这两棵树,但是我们可以通过在parse trees中统计上述两种树结构出现的次数来选取那一棵树,我们使用lexicalized PCFGs也可以做到这一点。
Lexicalized of a Treebank
见下图,a表示没有经过词汇标记的树,b表示使用Lexicalized标记的树: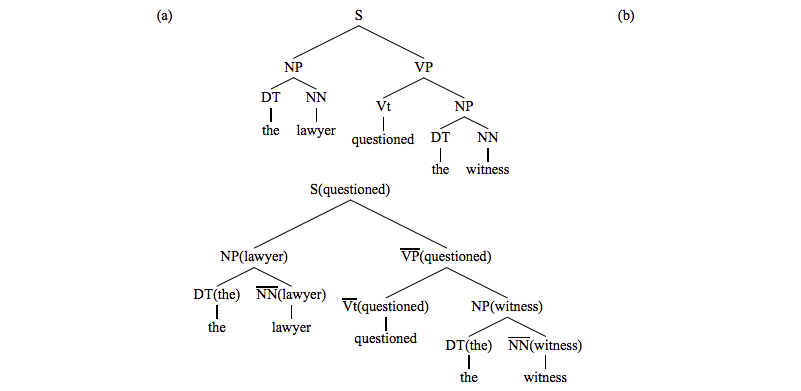
关于b图,父节点括号内的词是自底向上从孩子节点中选取head词,head词表示一个规则转换中的关键词,比如 用索引表示指定中哪个作为head词,在parse tree上用上划线表示,比如的h等于2,在VP上用上划线表示。
Lexicalized PCFGs
用Chmosky normal 形式定义,参数表示如下:
- N表示的是非终止符
- 其中表示词汇集合,也就是终止符
- R 是一个规则集合,这些规则属于下面三种中的一种:这里的h就是head,m就是modify,也就是要改变的单词
- 对每一个规则,用表示概率,有:
其中表示任何规则的左边
- 定义表示X的词汇是h的概率,有
这样parse tree的概率就可以如下表示,其中表示R中的规则:
如下图,就可以计算下面解析树的概率了: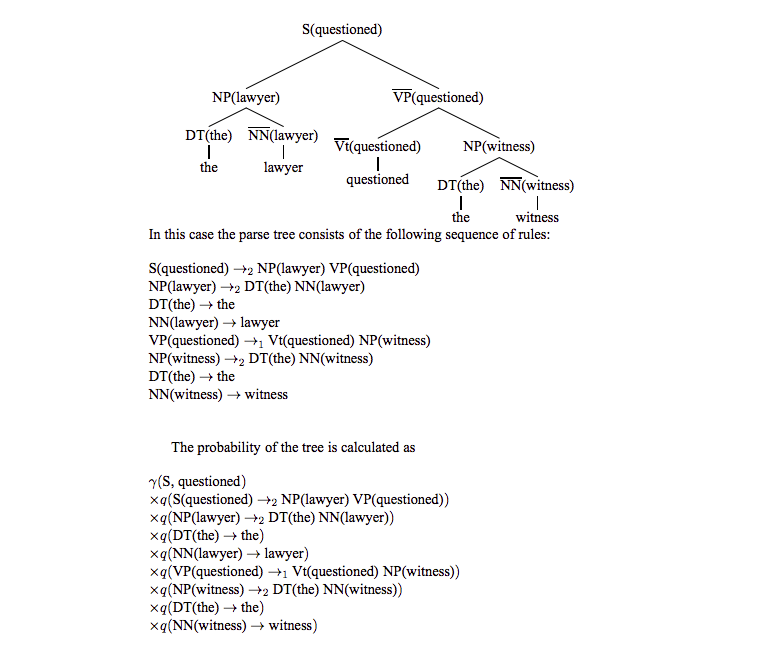
Parameter Estimation in Lexicalized PCFGs
举个例子,对于规则,写成概率形式如下:
最后一个式子是条件概率展开,分为两部分,这里使用平滑技术求解,可以想象成前面的3-gram模型,避免0的出现,第一部分用下面两个式子结合得到:
使用表示如下:
第二部分式子可以作如下等价:
继续使用平滑估计:
这样第二个式子使用就可以表示如下:
如上,就是对于规则的求解,那么一棵树的概率就可以通过这样的方式求解出来。最后当然是要找出一个概率最高的树了,下面讲到。
Parsing with Lexicalized PCFGs
和PCFGs的算法类似,定义表示对任意一棵以X为根节点,词汇索引为h,从i到j的单词串的树的最大概率,即和表示从第个单词到第个单词,表示在i到j这些单词中选择一个单词作为head,X表示树根,且其词汇信息为head。
给定初始条件:
通项公式如下图所示: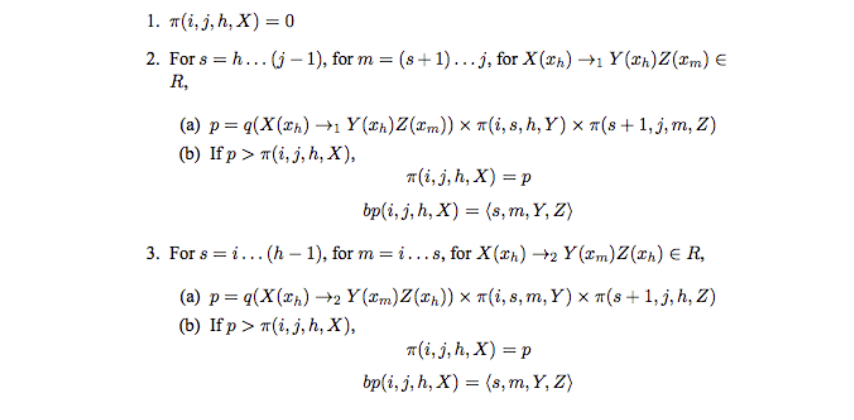
说明一下:m是下一个head对应的索引,有两种情况,一种是分解后,根的head落到第一部分,一种是分解后根的head落到第二部分,不过这里倒是默认分解为两部分。
算法如下图所示:

