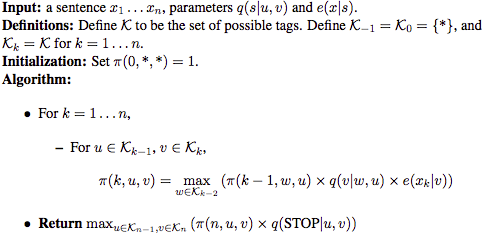NLP学习笔记之 Tagging Problems and Hidden Markov Models

主要学习资料是cs224n的notes和Michael Collins的notes，和宗成庆的统计自然语言处理，这里并不是一个完整的翻译笔记，而是在阅读的过程中对其中不懂的东西的一些解释，以及避免遗忘做的一些笔记，当然初入NLP，难免对一些知识理解不透或者有所偏差。

Introduction

对于一个句子，我们要做的是给每一个单词打上词性标记，比如句子the dog saw a cat对应的tag sequence是D N V D N，这个句子的长度是5，对应的输入$x_1=the,x_2=dog,x_3=saw,x_4=the,x_5=cat$，用$y_1y_2...y_n$来表示tagging model的output，对应上面的有$y_1=D,y_2=N,y_3=V,...$。匹配句子$x_1...x_n$的tag sequence $y_1...y_n$的问题叫做 sequence labeling problem 或者是 tagging problem。

Two Example Tagging Problems : POS Tagging and Named-Entity Recognition

前面讲到的就是POS Tagging，其有两大挑战，第一个是tagging的歧义问题，因为一个单词有可能是动词又有可能是名词；第二个是词库中的单词有限，导致训练例子中的单词可能在词库中没有出现，然后是Named-Entity Recognition，notes中提到的实体有PERSON,LOCATION,COMPANY。但是对这一块的讲解非常少，所以这里就不提了[后期如果有用会补上吧。]

Generative Models

这里主要是讲解隐马尔可夫模型应用在tagging问题上，这里以$x^{(i)}$作为句子，$y^{(i)}$作为对应的标签，我们的目的是在语料库集合$Y,y \in Y$中找到最符合句子$x^{(i)}$的标签$y^{(i)}$，即如下：

$$f(x)=arg \, \max_{y\in Y}\,\,p(y|x)$$

那么如何对于给定的$x^{(i)}$，在Y中找到最优的$y$呢，即如何求解p(y|x)呢，这里我们将上式转换一下，用贝叶斯公式求解：

$$p(y|x)=\frac{p(y)p(x|y)}{p(x)}$$

由于对于x而言，求解全部y的概率，因此p(x)可以看成常数，也就是求下面的最大值对应的y：

$$f(x)=arg \,\, \max_y p(y)p(x|y)$$

Generative Tagging Models

对于单词集$V$，标记集$K$，定义$S$为sequence/tag-sequence对$<x_1...x_n,y_1...y_n>$，对于$x_i \in V$，$y_i \in K$，有如下要求：

$$for\,\,any\,\, <x_1...x_n,y_1...y_n> \in S\\ p(x_1...x_n,y_1...y_n) >=0\\ \sum_{<x_1...x_n,y_1...y_n> \in S} p(x_1...x_n,y_1...y_n)=1$$

那么对于给定的一个生成标记模型，从序列$x_1...x_n$中标记出序列$y_1...y_n$被定义如下：

$$f(x_1...x_n)=arg\,\, \max_{y_1...y_n}\,\,p(x_1...x_n,y_1...y_n)$$

这里就是找出全部的序列$y_1...y_n$，其中$y_i \in K$，计算其中的概率值，将最大的概率值对应的序列$y_1...y_n$作为模型的输出。那么如何计算这个概率呢，下面有讲到。

Trigram Hidden Markov Models

这里是Trigram，也就是说序列中$y_i$只与$y_{i-1}$和$y_{i-2}$有关。
给出下面两个参数 ：
参数 $q(s|u,v)$：对于任意的trigram(u,v,s)，其中$s \in K \cup \{STOP\}, u,v \in K \cup \{*\}$，其概率$q(s|u,v)$可由在看到s在bigram (u,v)后的概率。
参数 $e(x|s)$：对于任意$x \in V, s \in K​$ 这个值可以表示为看见观测值x配对s的概率。
那么之前概率$p(x_1...x_n,y_1...y_{n+1})$可以表示如下：

$$p(x_1...x_n,y_1...y_{n+1})=p(y_1...y_{n+1})p(x_1...x_n|y_1...y_{n+1})\\ =\prod_{i=1}^{n+1} q(y_i|y_{i-2},y_{i-1}) \prod_{i=1}^{n} e(x_i|y_i)$$

这里有$y_{n+1}=STOP，y_0=y_{-1}=*$。
那么为什么上面这个公式成立呢，这里是有一些假设的，这里使用随机变量序列$X_1...X_n$和$Y_1...Y_n$，其中n为序列的长度，假设$X_i$可以取集合$V$中的任意的值，$Y_i$可以取集合$K$中任意一个标记，那么上式可以被定义为：

$$P(X_1=x_1...X_n=x_n,Y_1=y_1...Y_{n+1}=y_{n+1})\\ =\prod_{i=1}^{n+1}P(Y_i=y_i|Y_{i-2}=y_{i-2},Y_{i-1}=y_{i-1})\prod_{i=1}^{n}P(X_i=x_i|Y_i=y_i)$$

这里第一个连乘是没有问题的，但是第二个连乘是怎么得到的呢，下面一步步分析
这里先讲一下概率模型$P(X_1=x_1...X_n=x_n)$的求解，如下：

$$P(X_1=x_1...X_n=x_n)\\ =P(X_n=x_n|X_1=x_1...X_{n-1}=x_{n-1})P(X_1=x_1...X_{n-1}=x_{n-1})\\ 其中P(X_1=x_1...X_{n-1}=x_{n-1})\\ =P(X_{n-1}=x_{n-1}|X_1=x_1...X_{n-2}=x_{n-2})P(X_1=x_1...X_{n-2}=x_{n-2})\\ ...\\ P(X_1=x_1, X_2=x_2)=P(X_2=x_2|X_1=x_1)P(X_1=x_1)\\ 这样上面可以表示如下：\\ P(X_1=x_1...X_n=x_n)=\prod_{i=1}^{n}P(X_i=x_i|X_1=x_1...X_{i-1}=x_{i-1})$$

那么下面这个公式就知道怎么变来的了吧

$$P(X_1=x_1...X_n=x_n|Y_1=y_1...Y_{n+1}=y_{n+1})\\ =\prod_{i=1}^{n}P(X_i=x_i|X_1=x_1...X_{i-1}=x_{i-1},Y_1=y_1...Y_{n+1}=y_{n+1})$$

这里做了一个假设，变量$X_i$独立于之前的观测变量$X_1...X_{i-1}$和状态变量$Y_1...Y_{i-1},Y_{i+1}...Y_{n+1}$ ，当被给出变量$Y_i$时。那么上面的式子就变为：

$$\prod_{i=1}^{n}P(X_i=x_i|X_1=x_1...X_{i-1}=x_{i-1},Y_1=y_1...Y_{n+1}=y_{n+1})\\ =\prod_{i=1}^{n}P(X_i=x_i|Y_i=y_i)$$

Estimating the Parameters of a Trigram HMM

这里定义一下$c(s \to x)$为在语料库中标签s和单词x匹配的次数，那么上述的两个参数在语料库中的最大似然估计如下：

$$q(s|u,v)=\frac{c(u,v,s)}{c(u,v)}\\ e(x|s)=\frac{c(s \to x)}{c(s)}$$

同样对于在语料库中$q(s|u,v)$为0的情况，我们用上一章中讲到的解决，对于$e(x|s)$为0的情况，也就是说在语料库中没有出现该单词，这里notes中给出一种解决办法就是使用伪词(pseudo-words)[这块没有细看，后期用到再补]

Decoding with HMMs: the Viterbi Algorithm

那么知道如何求解$q(s|u,v)$和$e(x|s)$，我们又知道

$$p(x_1...x_n,y_1...y_{n+1})== \prod_{i=1}^{n+1} q(y_i|y_{i-2},y_{i-1}) \prod_{i=1}^{n} e(x_i|y_i)$$

而我们的原始问题是发现一组使概率值最大的序列$y_1...y_{n+1}$，即：

$$arg\,\, \max_{y_1...y_n}\,\,p(x_1...x_n,y_1...y_n)$$

这里举个例子，对于输入的句子the dog barks ，假设标记集为$K=\{D,N,V\}$，那么可能的标记序列$y_1y_2y_3y_4$可以是下面任意一种：

D	D	D	STOP
D	D	N	STOP
D	D	V	STOP
D	N	D	STOP
...

对于$|K|=3$时，有27种可能，如果计算这$3^3=27$种情况中的每一种，找出概率最大的那个序列，显然是不太现实的，我们需要用一种更为简化的方法来解决这个问题。
下面的维特比算法就给出这样一种解决办法，可以将时间复杂度由$O(|K|^n)$缩小到$O(n|K|^3)$，使用的方法是动态规划，就是对一个长度为n的句子分解，给定初始条件，给出通项公式，即求长度为i的子句最大概率下对应的子标记和长度为i-1的子句最大概率下对应的子标记的关系，这样就可以求出长度为n的原句最大概率下对应的标记。

VITERBI ALGORITHM
输入的句子是$x_1...x_n$，对任意的$k \in \{1...n\}$ ，任意的序列$y_{-1},y_{0},y_{1}...y_{k}$，且 $y_i \in K , y_{-1}=y_0=*$，定义如下函数：

$$r(y_{-1},y_0,y_1,...,y_k)=\prod_{i=1}^{k}q(y_i|y_{i-2},y_{i-1})\prod_{i=1}^{k}e(x_i|y_i)$$

这里举个例子如下：

$$p(x_1...x_n,y_1...y_{n+1})=r(*,*,y1,...,y_n) q(STOP|y_{n-1},y_n)$$

继续，定义$K_{-1}=K_{0}=\{*\}$和$K_k=K\,\,for\,\,k \in \{1...n\}$,定义$S(k,u,v)$为序列$y_{-1},y_{0},y_1,...,y_{k}$ 的集合，其中$u \in K_{k-1}, v \in K_{k},y_{k-1}=u,y_k=v$，定义：

$$\pi(k,u,v)= \max_{<y_{-1},y_0,y_1,...,y_k> \in S(k,u,v)} r(y_{-1},y_0,y_1,...,y_k)$$

给定初始条件：$\pi(0,*,*)=1$
给定通项公式：

$$\pi(k,u,v)=\max_{w \in K_{k-2}}\big(\pi(k-1,w,u)q(v|w,u)e(x_k|v)\big)$$

算法如下：