51. N-Queens

发表于 | 分类于 | 阅读次数

description

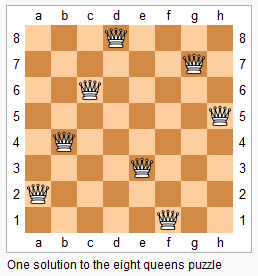
8-queens

  1. Given an integer n, return all distinct solutions to the n-queens puzzle.

Each solution contains a distinct board configuration of the n-queens’ placement, where ‘Q’ and ‘.’ both indicate a queen and an empty space respectively.

For example,
There exist two distinct solutions to the 4-queens puzzle:

1
2
3
4
5
6
7
8
9
10
11
[
 [".Q..",  // Solution 1
  "...Q",
  "Q...",
  "..Q."],
 ["..Q.",  // Solution 2
  "Q...",
  "...Q",
  ".Q.."]
]

  1. instead outputting board configurations, return the total number of distinct solutions

题意与解法

题目的意思是说，找出n皇后全部的解，即满足每一个棋子所在的行，列，对角线上都没有其他棋子

解法：

将问题变小，找相同的规律：即第i个棋子只能在第i行上选择，而且每次选择后都要判断是否满足条件；那么求第i个棋子的位置时遍历第i行上的点，判断是否满足条件，满足则判断第i+1行，直到i+1越界返回；回溯…

子问题是在第i行中找到满足条件的位置

满足条件的判断这里我用一个标志矩阵来记录，每当遍历第i行的下一个位置时，回溯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
public static List<List<String>> solveNQueens(int n) {
    boolean[][] flag=new boolean[n][n];//标志矩阵
    boolean[][] queen=new boolean[n][n];//皇后矩阵
    List<List<String>> lists=new ArrayList<>();
    return queenDfs(queen,flag,lists,0);
}
private static List<List<String>> queenDfs(boolean[][] queen, boolean[][] flag, List<List<String>> lists, int index) {
    //遍历到头
    if(index==queen.length){
        List<String> list=new ArrayList<>();
        for(int i=0;i<queen.length;i++){
            String s="";
            for(int j=0;j<queen.length;j++){
                if(queen[i][j]==true)s+="Q";
                else s+=".";
            }
            list.add(s);
        }
        lists.add(list);
        return lists;
    }
    //dfs,遍历第index行
    for(int j=0;j<queen.length;j++){
        if(flag[index][j]==true)continue;
        else queen[index][j]=true;
        //临时矩阵
        boolean [][] temp=new boolean[queen.length][queen.length];
        for(int k=0;k<queen.length;k++){
            for(int p=0;p<queen.length;p++){
                temp[k][p]=flag[k][p];
            }
        }
        //处理标志矩阵
        for(int k=0;k<queen.length;k++)flag[index][k]=true;//横
        for(int k=0;k<queen.length;k++)flag[k][j]=true;//竖
        for(int k=0;j+k<queen.length&&index+k<queen.length;k++)flag[index+k][j+k]=true;//东南
        for(int k=1;j-k>=0&&index-k>=0;k++)flag[index-k][j-k]=true;//西北
        for(int k=1;index-k>=0&&j+k<queen.length;k++)flag[index-k][j+k]=true;//东北
        for (int k=0;index+k<queen.length&&j-k>=0;k++)flag[index+k][j-k]=true;//西南
        lists=queenDfs(queen,flag,lists,index+1);
        //回溯
        queen[index][j]=false;
        for(int k=0;k<queen.length;k++){
            for(int p=0;p<queen.length;p++){
                flag[k][p]=temp[k][p];
            }
        }
    }
    return lists;
}

关于第2问：返回n皇后的可能数

这里直接用一个num记录即可，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
public static int totalNQueens(int n) {
    boolean[][] flag=new boolean[n][n];
    boolean[][] queen=new boolean[n][n];
    return queenDfs(queen,flag,0);
}
private static int queenDfs(boolean[][] queen, boolean[][] flag, int index) {
    if(index==queen.length){
        return 1;
    }
    int num=0;
    for(int j=0;j<queen.length;j++){
        if(flag[index][j]==true)continue;
        else queen[index][j]=true;
        boolean [][] temp=new boolean[queen.length][queen.length];
        for(int k=0;k<queen.length;k++){
            for(int p=0;p<queen.length;p++){
                temp[k][p]=flag[k][p];
            }
        }
        for(int k=0;k<queen.length;k++)flag[index][k]=true;//横
        for(int k=0;k<queen.length;k++)flag[k][j]=true;//竖
        for(int k=0;j+k<queen.length&&index+k<queen.length;k++)flag[index+k][j+k]=true;//东南
        for(int k=1;j-k>=0&&index-k>=0;k++)flag[index-k][j-k]=true;//西北
        for(int k=1;index-k>=0&&j+k<queen.length;k++)flag[index-k][j+k]=true;//东北
        for (int k=0;index+k<queen.length&&j-k>=0;k++)flag[index+k][j-k]=true;//西南
        num+=queenDfs(queen,flag,index+1);
        queen[index][j]=false;
        for(int k=0;k<queen.length;k++){
            for(int p=0;p<queen.length;p++){
                flag[k][p]=temp[k][p];
            }
        }
    }
    return num;
}
如果觉得有帮助，给我打赏吧！