简介
非对称加密
非对称加密:两个密钥,一个公钥,一个私钥,如果用公钥加密的数据只有用私钥才能解密,用私钥加密的数据只有公钥才能解密
特点:算法强度复杂,安全性能高,导致加密速度慢
主要算法:RSA,Elgamal,背包算法,Rabin,D-H,ECC,
对称加密
双方使用同样的密钥加解密,这个是有一个问题的,首先得保证密钥不被泄露,而且需要定期在通信网络的源端和目的端同时修改密钥
密钥越大,加密越强,但加密与解密的过程越慢
主要算法:DES,3DES,IDEA,AES
非对称加密算法介绍
RSA
首先给出两个已知公式
欧拉函数:表示小于n的正整数中,有多少个与n构成互质关系,其中 表示任何一个大于1的整数都可以写成多个质数次方的积
欧拉定理:如果a,n互质,则下面公式成立:
RSA的公钥私钥选取过程
选取两个不相等的质数p和q
计算乘积n=p*q,其中n转为二进制的长度即为密钥的长度
计算$\phi(n)$
因为p和q为质数,不能分解,因此代入欧拉函数得到:
在{}中选取e
计算d
计算出一组满足上式的整数解(d,k)
将(n,e)封装为公钥,(n,d)封装为私钥
加解密及私钥解密证明
要加密信息为m ,m为整数(转换)且m
加密:$m^{e}=c\,\,(mod\,\,n)$
计算出c,作为密文发送出去
解密:$c^{d}=m\,\,(mod\,\,n)$
计算出m,即为明文
证明过程如下:
由加密的式子可得:
将c代入解密的式子,得到:
由$ed\,\,\%\,\,\phi(n)=1$ 即:$ed=h\phi(n)+1$ ,上式变为:
对于上式,如果m和n互质,根据欧拉定理:
如果m和n不互质,即说明m和n存在非1的公因子,由于n=pq,且p,q均为质数,说明n的非1因子是p,q;
那么m必然是p得倍数或者是q得倍数,设$m=kp$
由于m<n,可得k<q,即k与q互质,那么kp和q互质,由欧拉定理得:
RSA算法的可靠性:
公钥开放,也就是说如果知道了d,私钥就泄露了
由上面第一个式子,要想知道d,必须知道$\phi(n)$ ,而$\phi(n)$由第二个式子可知,与p和q相关,由第三个式子知道p和q是n的因式分解
因此如果想破解RSA算法,必须知道满足$pq=n$的所有质数对(p,q),即如果高效解决大整数的因式分解就能快速破解RSA算法
D-H密钥交换
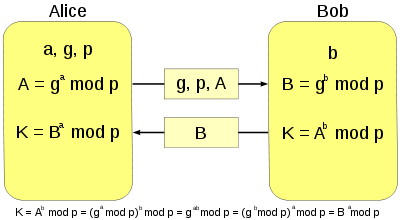
a为Alice的私钥,b为Bob的私钥,公开的时g,p,A,B,密钥为K
原理就是通过自己的私钥运算,并发送公钥给对方,通过运算获取相同的密钥,使用对称加密来加密明文
证明
可靠性
要知道K,需要知道$g^{ab}\,\,mod\,\,p$ ,即需要知道a和b,而a和b分别由下式得到:
上式是离散对数问题,目前没有快速求解离散对数的算法
ElGamal加密算法
实质上就是将D-H算法变为非对称加密算法
密钥生成
选择素数p,两个随机数g和x,满足g,x<p,
计算 y=$g^x\,\, mod \,\,p$
私钥为x
公钥为y,g,p,
加密
随机选择k,满足k与p-1互素
其中M为明文,(a,b)为密文
解密
可靠性
同D-H算法,是离散对数难题
ECC加密算法
椭圆曲线:
- 关于X轴对称
- 画一条直线跟椭圆曲线相交,它们最多有三个交点
椭圆曲线上的运算:
加法运算:
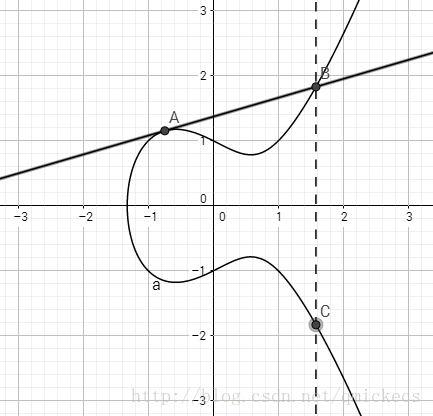
设椭圆曲线上有两点,A和B,作这两点的直线与该曲线相交于第三点C,将C点关于X轴对称得到D点
记D=A+B
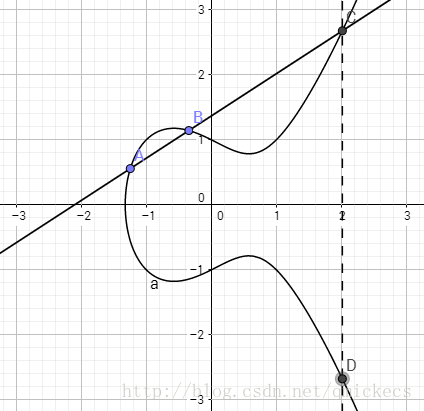
当A和B重合时,即作A点的切线,与曲线相交于第二点(B点),然后关于X轴对称得到C点
记 C=A+A
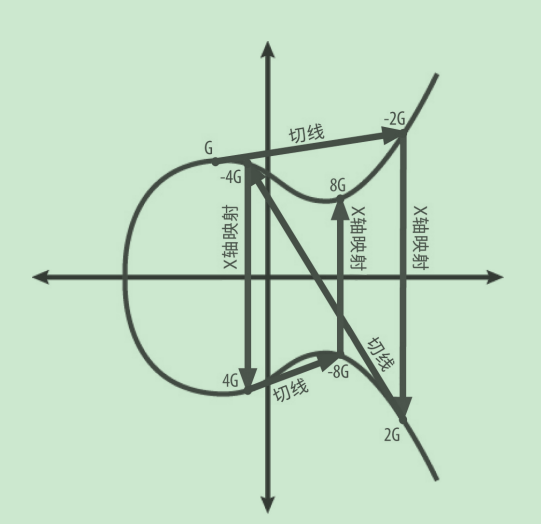
乘法运算
转为加法运算
如下图所示:
椭圆曲线上点的阶:
P为椭圆曲线上的点,如果nP=无穷远点,n取最小整数,即为P的阶
无穷远点:如果椭圆曲线上的两点A,B的连成的直线不与椭圆曲线交于第3点,则有A+B=无穷远点
椭圆曲线在密码学中的应用
对于实数域上的椭圆曲线,做如下变化:
- 实数域中取整数点
- 对整数点取模处理
如下,对一椭圆曲线 mod 17的结果
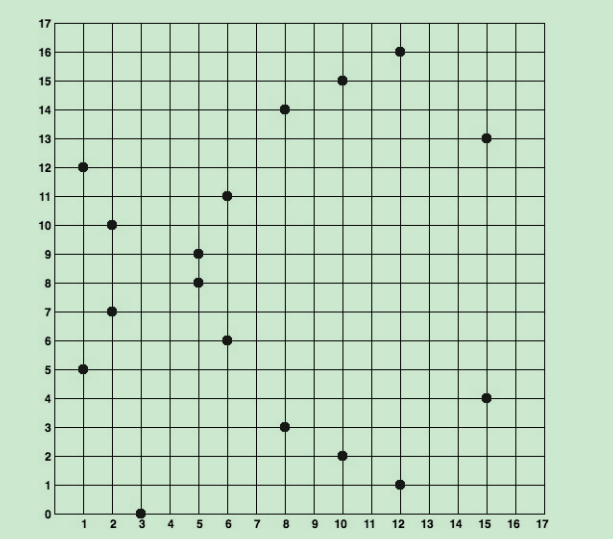
对于椭圆曲线中的运算仍然成立,如下图所示,描述C=A+B的过程

有限域椭圆曲线上的加解密
用户A作如下处理:
在椭圆曲线上选取一基点G,椭圆曲线$E_{p}(a,b)$ ,选取整数k作为私钥(k小于n,n为G的阶),
计算K=kG
将G,K,$E_{p}(a,b)$ 作为公钥公开
用户B要将明文M传给A,作如下处理:
随机产生一个随机数r,(r<n)
计算点
将传给用户A
用户A接收到后作如下处理:
证明:
可靠性
已知K和G,如何求解k的问题:对于椭圆曲线上的kG运算是不可逆的,这是椭圆曲线上的离散对数问题,目前无法找到快速解决该问题的方法。
实际的函数如下:
|
|
有个问题:具体的kG如何计算?,为什么不可逆?
以下只是猜测,并没有找到什么确切的答案
原因:比如k=17,加密的时候因为知道k,作如下运算,由G得到2G,由2G得到4G,由4G得到8G,由8G得到16G,16G再和1G运算得到17G,总共走了5步;而如果破解的话,需要一步一步遍历,如果作倍数运算可能会漏掉k,导致永远找不到,因此只能有1G得2G,由2G得3G,…直到17G,最后的结果是走了17步;而如果k很大,结果会更明显;已知k的运算时间复杂度为O(log n),未知k的时间复杂度为O(n)
更者,如果17G不等于17G(即不同的叠加出现不同的17G),那么就有更多的可能了
背包算法
超递增背包:其中的每一项都大于它之前所有项之和
记超递增背包为{}
选取N满足N与背包中的任何一个数没有公因子
并取一个模数M,满足该模数比背包中的所有数的和都大
对背包中的每个元素作如下运算:
将修改后的背包{}作为公钥,原始的超递增背包{}作为私钥
加密
对于要加密的二进制消息,按照背包个数分组,然后将每组二进制消息中1对应的背包元素相加,将每组最后相加的结果{}作为密文发送出去
解密
计算$N^{-1}$ : 满足$N\,\,N^{-1}\,\,mod\,\,M=1$
对密文做如下运算
最后将在背包中的位置映射到二进制上,即得到了二进制消息
证明
对于一组二进制消息来说,假设第i,j…等位上为1,加解密的运算如下:
前提条件M的选取使得倒数第二行求和的结果和最后一行相等,超递增背包使得最后一个等式唯一
可靠性
公钥为{},M,N,得到密文后,可以将每组的 的和s求出来
由公钥的求解方法,我们可以得到一个矩阵,矩阵的第i行表示私钥中第i个元素所有可能的取值,即私钥一定由下面的矩阵中每一行选取一个值组成:
需要k重for循环进行遍历,每次选取元素时需满足该背包为超递增背包,选取完k个元素后,将得到的背包用于计算密文,如果所有的密文均可以由得到的背包中的元素组成,则该背包为密钥
时间复杂度为$O(m^k)$,m为矩阵的宽
举个例子:
取一个超递增序列{2,3,6,13,27,52},N=31,M=105
公钥为{62,93,81,88,102,37},N=31,M=105
加密过程:
需要传递的明文为011000110101101110,按照背包的大小分为三组:011000 110101 101110
011000 对应 93+81=174
110101 对应 62+93+88+37=280
101110 对应 62+81+88+102=333
密文为{174,280,333}
解密过程:
求解$N^{-1}=61$
对于超递增背包,上面求解的结果都会唯一对应一组背包中的数字
Rabin
选取两个素数p,q,满足同余3模4. 作为私钥,n=pq作为公钥
加密消息M:
解密:
由于n=pq,由中国剩余定理得到$M^2=C\,\,(mod\,\,n)$等价为:
引入符号Legendre$\left [ \frac{a}{p} \right ]$:假设p为一个奇素数,a为一个整数,那么有
对于同余方程式$x^2\equiv a(mod\,\,q)$,如果Legendre符号$\left [ \frac{a}{p} \right ]=1$,且$p\equiv3(mod\,\,4)$
则方程式的解为
由模n二次剩余问题的定理1可以证明$\left [ \frac{C}{p} \right ]=1$,$\left [ \frac{C}{q} \right ]=1$
则4个解分别为:
从中选择一个,从中选择一个,有4种组合方式,由之前的等价公式合并,利用中国剩余定理求解M的值
可以得到4个值,其中有一个就是M,需要在消息加密前加入一个已知的标题,以确定M
可靠性
基于求合数n的模平方根难度,解密过程在已知合数为pq的条件下,使用一种数学方法来得到M
对称加密算法
DES
DES是基于组块的加密算法,输入输出均为64位长度
加密过程:
密钥K转为二进制64位,根据表格PC-1变换为56位,拆为左右两半部分 ,每半边28位
对进行左移,对于前一个来说左移位数按照1,1,2,2,2,2,2,2,1,2,2,2,2,2,2,1进行,最后得到 16组子密钥
将拼接,并对应到表格PC-2,得到 为48位,$1\leqslant i \leqslant 16$
将明文M转为二进制,并按照IP表变换,记为ip,将ip的左半部分32位记为,右半部分32位记为
使用函数$f$执行16次迭代:
具体$f$中先将从32位扩展为48位,按照表E;然后进行异或运算:,记为 ;再将进行S运算,即 ,的运算原理是计算中第一位和最后一位的组成的二进制值作为i,中间的二进制值作为j,在中对应的第i行第j列的值转为二进制,最后输出的 再由表P转为32位的输出
将得到的逆转结合得到一个64位的区块: ;将其按表IP-1输出写为16进制即为明文加密后的结果
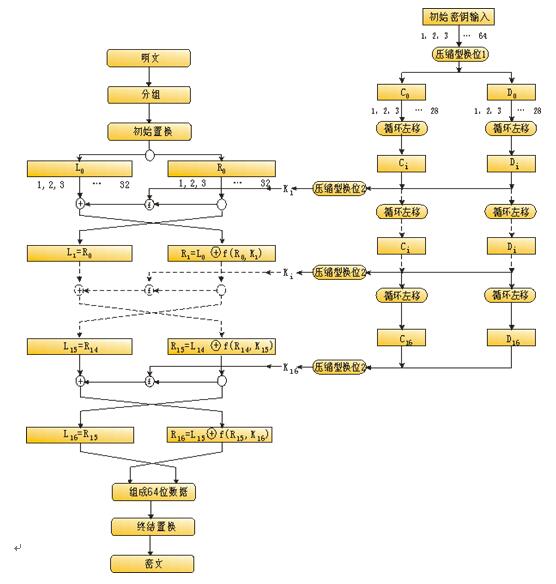
解密过程
和加密一样,只是在16轮迭代过程中,调转左右子密钥的位置
破解
如果不知道明文,只知道密文,是否能破解?
明文的组合方式是$2^{64}$种,密钥的组合方式是$2^{56}$ ,从中选取一种明文,一种密文,使得最后加密的结果恰好为密文,总共需要遍历$2^{64}*2^{56}$次
知道少量的明文密文对,是否能唯一确定一个密钥?
3DES
三重DES实质上将暴力破解难度从$2^{56}$变为$2^{168}$
使用3条56位的密钥对 数据进行三次加密。3DES(即Triple DES)是DES向AES过渡的加密算法
其具体实现如下:设Ek()和Dk()代表DES算法的加密和解密过程,K代表DES算法使用的密钥,P代表明文,C代表密文,这样:
3DES加密过程为:C=Ek3(Dk2(Ek1(P)))
3DES解密过程为:P=Dk1(EK2(Dk3(C)))
假设三个密钥均不相同,则本质上就相当于用一个长为168位的密钥进行加密
AES
分组密码,由于DES的密钥长度只有56位,而且随着计算机处理能力越来越强,DES变得不再安全,AES便出现了,用以取代DES
AES分组的长度有128位,192位,256位,下面是按照128位来讲解
加密
- 16字节的明文和扩展密钥异或,i=0
- 将上一步的结果映射到S盒,得到变换后的16字节
- 将上一步的16字节按照4x4的矩阵排列,对每一行按照0位,8位,16位,24位进行循环移位
- 将上一步得到的矩阵左乘指定矩阵A 得到新的矩阵
- 通过G函数获取下一个扩展密钥,将上一步的矩阵从新排成一列,与扩展密钥异或,i++
- 如果i=10,返回得到的16字节作为密文,否则执行第2步
解密
加密的逆过程
加解密如下图
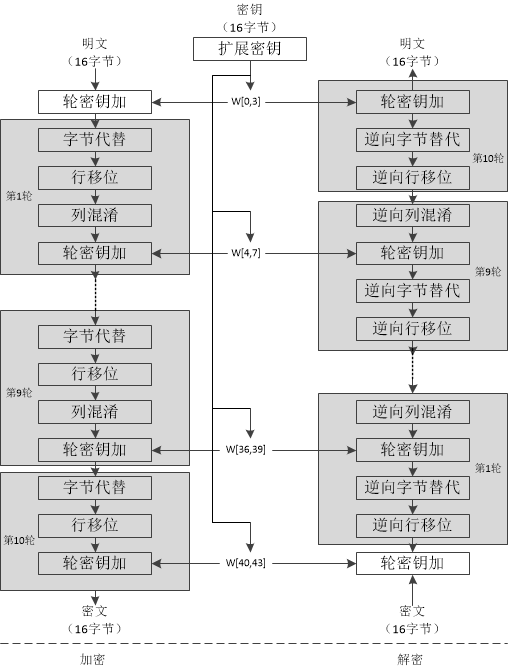
扩展密钥原理
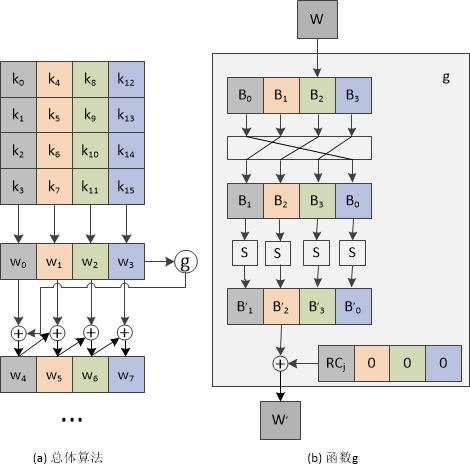
关于对称加密
对称加密的安全性基于密钥的长度,如果说一种情况出现:不管密钥的长度变为多长,计算机都能在很短的时间遍历完这所有的可能,该怎么办?
SSL
SSL 简述
HTTP+SSL=HTTPS
SSL在协议模型中的位置

SSL作用:
不使用SSL的HTTP通信,带来三大风险:窃听风险,篡改风险,冒充风险
使用SSL后,所有信息都是加密传播,第三方无法窃听;具有校验机制,被篡改,通信双方会立即发现;配备身份证书,防止被冒充
SSL握手过程
- 客户端发送请求:
生成的随机数n1,请求加密的方法…
- 服务器返回信息:
生成的随机数n2,确定加密方法,含公钥的数字签名…
- 客户端验证,回应:
对生成的随机数n3使用公钥加密,前面内容的hash值供校验
- 服务器回应:
前面内容的hash值,供客户端校验
n1,n2,n3用于生成会话密钥
白话数字签名
假设A和B通信,A需要将信息M发送给B这样一个问题:
如果使用对称加密,首先得传密钥吧,那还得使用非对称加密,那非对称加密的公钥开放,谁都可以使用,那A使用B的公钥将信息加密,传给B,而此时C也使用B的公钥将信息加密,传给B,B怎么确定哪个是A发过来的呢?
数字签名的验证功能:
B先随机生成一串数字发送给A,然后A用自己的私钥加密,再发送给B,B使用A的公钥解密得到的结果如果和随机数相等,则表明对方是A,因为A的公钥只能解用A的密钥加密的密文,其他伪造的密文,A的公钥无法解开。
数字签名的防篡改功能:
假设A需要发送一条消息给B,如何防止B篡改呢?
A使用自己的私钥加密消息,将消息发送给B,B使用A的公钥解密消息,只能知道消息的内容,无法修改消息,因为B修改消息后,并不知道A的私钥,无法加密消息
那么有一个很大的文件,需要发送,使用非对称加密太耗时,如何做:
数字签名:摘要算法+非对称加密
文件传输:对称加密+非对称加密
实际对文件进行数字签名:先使用摘要算法将文件生成唯一的散列值,然后用私钥对这个散列值进行加密,再把加密后的结果和明文一起发送到B,B此时在网上下载A的公钥进行解密,B再使用摘要算法将明文文件转为散列值,如果两个值相等,表明签名成功

