比较排序

发表于 | 分类于 | 阅读次数

问题描述

  1. 选择排序
  2. 插入排序
  3. 希尔排序
  4. 归并排序
  5. 快速排序
  6. 堆排序

解决方案

选择排序

排序思路：从第一个元素遍历数组，将最小的和第一个元素交换；从第二个元素遍历数组，将最小的和第二个元素交换…直至最后一个

1
2
3
4
5
6
7
8
9
10
11
12
#选择排序
def selection_sort(a):
    for i in range(len(a)):
        k=i
        for j in range(len(a))[i:]:
            if a[k]>a[j]:
                k=j
        t=a[i]
        a[i]=a[k]
        a[k]=t
    return a

选择排序的时间复杂度T(n)=n+(n-1)+(n-2)+…+1 ~ O(n^2)

插入排序

插入排序的一般思路是：以第一个元素为有序集，遍历其他元素，与有序集比较，找到该元素的放置位置，然后插入，下面是经典的方法，前面是先找到位置，然后再移位，而下面在比较的时候直接移位
以第一个元素开始为一个有序集，后面的元素a[j]与有序集从最后a[i]往前依次开始比较，如果小于，比较的元素右移(a[i]->a[i+1])，否则将该元素a[j]置于此a[i+1]

1
2
3
4
5
6
7
8
9
10
#插入排序的经典方法
def insert_sort(arr):
    for i in range(len(arr)-1):
        j=i+1
        t=arr[j]
        while i>=0 and arr[i]>t:
            arr[i+1]=arr[i]
            i=i-1
        arr[i+1]=t
    return arr

插入排序最坏的时间复杂度T(n)=1+2+…(n-1) ~ O(n^2)

希尔排序

希尔排序是插入排序的改进版，想象这么一种极端情况，待排序列的最后一个元素是最小的，这样插入排序需要将前面的所有元素往后移，才能把最后一个元素放进有序列中；而希尔排序就是针对这样的情况出现的
算法如下：
令k=n (n为序列中元素的个数)
第一步：取步长为k=k/2(可以按照其他方式选取)
第二步：对第i，i+k,i+k*2,…的元素排序，i小于k,这样的序列集有k个
第三步：执行第一步，当k=0时，跳出
如下图：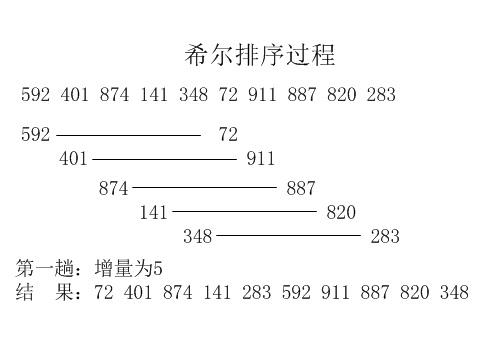
170426a
代码如下，需要借助快速排序函数insert_sort()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#希尔排序
def shell_sort(arr):
    n=len(arr)
    k=1#k为步长
    #步长k取通项公式an=i*3+1组成的序列中最大的小于n的数
    while(k<int(n/3)):
        k=k*3+1
    while k>=1:
        for i in range(k):
            t=insert_sort(arr[i::k])#以k为步长，获取arr中的元素组成序列传给插入排序
            p=i
            #将排好的序列赋值给指定的位置
            for j in t:
                arr[p]=j
                p=p+k
        #减小步长，继续排序
        k=int(k/3)
    return arr

希尔排序时间复杂度是要小于插入排序的，暂时不知道如何计算
动态图

![170426b](/upload/essayimage/170426b.gif)

归并排序

归并排序的思路是分治法
算法导论p17中提到
分解原问题为若干子问题，这些子问题是原问题规模较小的实例
解决这些子问题，递归求解各子问题
合并这些子问题的解成原问题的解
具体思路：将n个元素的列表分解为两组n/2个元素的列表，继续分解，直到只有一个元素，返回，执行合并函数，对两组有序列进行排序;需要开辟一个O(n)的空间来存储n个元素,而对原arr数组修改

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#将两个有序列表归并为一个有序列表
def merge(arr,p,mid,r):
    for i in range(r-p+1):
        temp[p+i]=arr[p+i]
    i=p
    k=p
    j=mid+1
    while i<=mid and j<=r:
        if temp[i]<temp[j]:
            arr[k]=temp[i]
            i=i+1
            k=k+1
        else:
            arr[k]=temp[j]
            j=j+1
            k=k+1
    if i<=mid:
        while i<=mid:
            arr[k]=temp[i]
            i=i+1
            k=k+1
    elif j<=r:
        while j<=r:
            arr[k]=temp[j]
            j=j+1
            k=k+1
#归并排序
def merge_sort(arr,p,r):
    if p>=r:
        return
    mid=p+int((r-p)/2)
    merge_sort(arr,p,mid)
    merge_sort(arr,mid+1,r)
    merge(arr,p,mid,r)
    return arr

时间复杂度T(n)=O(nlgn)
动态图

![170426c](/upload/essayimage/170426c.gif)


快速排序

和归并的思想是一样的，只是快速排序是原址排序
思路：给定一个数组，取最后一个元素作为比较的对象，将其它元素与之相比，小者置于该元素的左边，大者置于该元素的右边；将由这个元素分开的两个数组继续进行上述操作…,当数组元素为一个时不再执行该操作。
【notice】其中涉及到如何将小的元素置于比较对象的左边，将大的元素置于比较对象的右边的问题：
书中是这样写的：一个指针i遍历数组，一个指针j记录小的元素最后位置的后一个，如果有小的元素，则交换j指向的元素和i指向的元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#a为数组；p，r为数组第元素的下标
def quick_sort(a,p,r):
    if p<r:
        q=partition(a,p,r)
        quick_sort(a,p,q-1)
        quick_sort(a,q+1,r)
def partition(a,p,r):
    i=p
    j=p
    while i<r:
        if a[i]<a[r]:
            temp=a[i]
            a[i]=a[j]
            a[j]=temp
            j=j+1
        i=i+1
    temp=a[j]
    a[j]=a[r]
    a[r]=temp
    return j

堆排序

这里就采用数组来表示堆，结构如下所示：

1
2
3
4
5
6
def parent(i):
    return int(i/2)
def left(i):
    return 2*i
def right(i):
    return 2*i+1

这里实现的是最大堆，最小对同理
堆排序的核心是如何维护堆，即对于树上的某个元素i，假设i后面的元素已经符合最大堆，如何让i也符合最大堆；（有点归纳的感觉）
维护最大堆：这是一个递归的过程，对于i，i的左节点，i的右节点，将最大的值和i交换，如果被交换的是子节点，则继续遍历子节点，直到没有子节点。
如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#维护最大堆，已知i元素后的元素是符合最大堆的，目的是使i元素也符合最大堆，
#前提是i下的子树均符合最大堆
#a为数组，i为可能不符合最大堆的元素
def max_heapify(a,i):
    lindex=left(i)
    rindex=right(i)
    largest=i
    if lindex<len(a) and a[lindex]>a[largest]:
        largest=lindex
    elif rindex<len(a) and a[rindex]>a[largest]:
        largest=rindex
    if largest!=i:
        if largest==lindex:
            temp=a[i]
            a[i]=a[lindex]
            a[lindex]=temp
        else:
            temp=a[i]
            a[i]=a[rindex]
            a[rindex]=temp
        max_heapify(a,largest)

建堆
先是找到含有子节点且离根节点最远的节点，就是len(a)/2，然后向上遍历到根节点

1
2
3
4
5
6
#建堆
def build_max_heap(a):
    i=int(len(a)/2)
    while i>=0:
        max_heapify(a,i)
        i=i-1

输出堆

1
2
3
4
5
6
7
8
9
10
11
12
13
#将堆中的元素取出并赋值给asort
def heapsort(a):
    build_max_heap(a)
    asort=[]
    i=len(a)-1
    while i>=2:
        asort.append(a[0])
        a[0]=a[i]
        a.pop(i)
        max_heapify(a,0)
        i=i-1
    asort.append(a[0])
    asort.append(a[1])

[注]
图片来源于http://blog.jobbole.com/11745/

如果觉得有帮助，给我打赏吧！